【题目】某校九年级(1)班所有学生参加2010年初中毕业生升学体育测试,根据测试评分标准,将他们的成绩进行统计后分为A、B、C、D四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题: 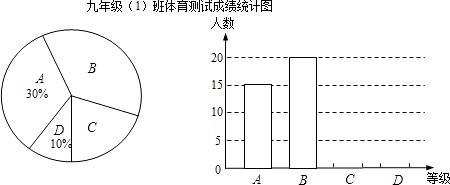
(1)九年级(1)班参加体育测试的学生有人;
(2)将条形统计图补充完整;
(3)在扇形统计图中,等级B部分所占的百分比是 , 等级C对应的圆心角的度数为;
(4)若该校九年级学生共有850人参加体育测试,估计达到A级和B级的学生共有人.
参考答案:
【答案】
(1)50
(2)解:D等的人数=总人数×D等比例=50×10%=5人,
C等人数=50﹣20﹣15﹣5=10人,
如图:
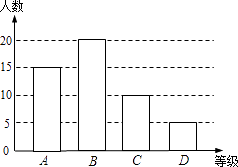
(3)40%;72°
(4)595
【解析】(1.)总人数=A等人数÷A等的比例=15÷30%=50人; (3.)B等的比例=20÷50=40%,
C等的比例=1﹣40%﹣10%﹣30%=20%,
C等的圆心角=360°×20%=72°;
(4.)估计达到A级和B级的学生数=(A等人数+B等人数)÷50×850=(15+20)÷50×850=595人.
(1)由A等的人数和比例,根据总数=某等人数÷所占的比例计算;(2)根据“总数=某等人数÷所占的比例”计算出D等的人数,总数﹣其它等的人数=C等的人数;(3)由总数=某等人数÷所占的比例计算出B等的比例,由总比例为1计算出C等的比例,对应的圆心角=360°×比例;(4)用样本估计总体.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在正方形ABCD中,点E、F在BD上,且AB=BE=DF.
(1)求证:四边形AECF是菱形;
(2)若正方形的边长为2,求四边形AECF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,E、F分别是AB、CD的中点,AF与DE相交于点G,CE与BF相交于点H.
(1)求证:四边形EHFG是平行四边形;
(2)□ABCD应满足什么条件时,四边形EHFG是矩形?并说明理由;
(3)□ABCD应满足什么条件时,四边形EHFG是正方形?(不要说明理由).

-
科目: 来源: 题型:
查看答案和解析>>【题目】将△ABC的边AB绕点A顺时针旋转α得到AB′,边AC绕点A逆时针旋转β得到AC′,α+β=180°.连接B′C′,作△AB′C′的中线AD.
(初步感知)
(1)如图①,当∠BAC=90°,BC=4时,AD的长为______;
(探索证明)
(2)如图②,△ABC为任意三角形时,猜想AD与BC的数量关系,并证明;
(应用延伸)
(3)如图③,已知等腰△ACB,AC=BC=m,延长AC到D,延长CB到E,使CD=CE=n,将△CED绕C顺时针旋转一周得到△CE′D′,连接BE′、AD′,若∠CBE′=90°,求AD′的长度(用含m、n的代数式表示).



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E、F分别是矩形ABCD的边BC、CD的中点,连接AC、AF、EF,若AF⊥EF,AC=
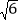 ,则AB的长为_____.
,则AB的长为_____.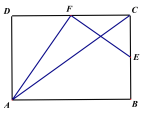
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知数轴上两点A,B对应的数分别是﹣1,3,点P为数轴上的一动点,其对应的数为x

(1)A、B两点的距离AB= ;
(2)在数轴上是否存在点P,使PA+PB=6?若存在,请求出x的值;若不存在,请说明理由.
(3)如图2,若点P以每秒1个单位的速度从点O出发向右运动,同时点A以每秒5个单位的速度向左运动,点B以每秒20个单位的速度向右运动,在运动的过程中,M、N分别是AP、OB的中点,问:
 的值是否发生变化?请说明理由.
的值是否发生变化?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】张家界市为了治理城市污水,需要铺设一段全长为300米的污水排放管道,铺设120米后,为了尽可能减少施工对城市交通所造成的影响,后来每天的工作量比原计划增加20%,结果共用了27天完成了这一任务,求原计划每天铺设管道多少米?
相关试题

