【题目】综合题。
(1)计算:﹣12016+(﹣5)×[(﹣2)3+2]﹣(﹣4)2÷(﹣ ![]() )
)
(2)解方程:x﹣ ![]() =2﹣
=2﹣ ![]()
(3)已知:A= ![]() a﹣2(a﹣
a﹣2(a﹣ ![]() b2),B=﹣
b2),B=﹣ ![]() a+
a+ ![]() b2 , 且|a+2|+(b﹣3)2=0,求2A﹣6B的值.
b2 , 且|a+2|+(b﹣3)2=0,求2A﹣6B的值.
参考答案:
【答案】
(1)解:原式=﹣1+30+32=61
(2)解:去分母得:6x﹣3x+3=12﹣2x﹣4,
移项合并得:5x=5,
解得:x=1
(3)解:∵|a+2|+(b﹣3)2=0,
∴a+2=0,b﹣3=0,
解得:a=﹣2,b=3,
则2A﹣6B=2( ![]() a﹣2(a﹣
a﹣2(a﹣ ![]() b2)﹣6(﹣
b2)﹣6(﹣ ![]() a+
a+ ![]() b2)=a﹣4a+
b2)=a﹣4a+ ![]() b2+4a﹣b2=a+
b2+4a﹣b2=a+ ![]() b2=﹣2+3=1
b2=﹣2+3=1
【解析】(1)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;(3)把A与B代入原式,去括号合并得到最简结果,利用非负数的性质求出a与b的值,代入计算即可求出值.
【考点精析】本题主要考查了解一元一次方程的步骤和有理数的四则混合运算的相关知识点,需要掌握先去分母再括号,移项变号要记牢.同类各项去合并,系数化“1”还没好.求得未知须检验,回代值等才算了;在没有括号的不同级运算中,先算乘方再算乘除,最后算加减才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据-5,-3,-3,0,1,3的众数是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.
(1)求抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,连结BD,求直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD?如果存在,请求出点P的坐标;如果不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条直线上任取一点A,截取AB=20cm,再截取AC=18cm,M、N分别是AB、AC的中点,则M、N两点之间的距离为cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏东33°方向,同时又位于B船的北偏东78°方向.
(1)求∠ABC的度数;
(2)A船以每小时30海里的速度前去救援,问多长时间能到出事地点.(结果精确到0.01小时).
(参考数据:
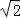 ≈1.414,
≈1.414,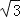 ≈1.732)
≈1.732)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市一月份的营业额为10万元,一至三月份的总营业额为45万元,若平均每月的增长率为x,则依题意列方程为( )
A. 10(1+x)2=45B. 10+10×2x=45
C. 10+10×3x=45D. 10[1+(1+x)+(1+x)2]=45
-
科目: 来源: 题型:
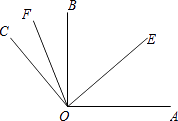
查看答案和解析>>【题目】如图,已知∠AOB=90°,∠EOF=60°,OE平分∠AOB,OF平分∠BOC,求∠AOC和∠COB的度数.
相关试题

