【题目】如图,已知∠AOB=90°,∠EOF=60°,OE平分∠AOB,OF平分∠BOC,求∠AOC和∠COB的度数. 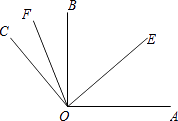
参考答案:
【答案】解:∵OE平分∠AOB,OF平分∠BOC, ∴∠BOE= ![]() ∠AOB=
∠AOB= ![]() ×90°=45°,∠COF=∠BOF=
×90°=45°,∠COF=∠BOF= ![]() ∠BOC,
∠BOC,
∵∠BOF=∠EOF﹣∠BOE=60°﹣45°=15°,
∴∠BOC=2∠BOF=30°;
∠AOC=∠BOC+∠AOB=30°+90°=120°
【解析】根据角平分线的定义得到∠BOE= ![]() ∠AOB=45°,∠COF=∠BOF=
∠AOB=45°,∠COF=∠BOF= ![]() ∠BOC,再计算出∠BOF=∠EOF﹣∠BOE=15°,然后根据∠BOC=2∠BOF,∠AOC=∠BOC+∠AOB进行计算.
∠BOC,再计算出∠BOF=∠EOF﹣∠BOE=15°,然后根据∠BOC=2∠BOF,∠AOC=∠BOC+∠AOB进行计算.
【考点精析】利用角的平分线对题目进行判断即可得到答案,需要熟知从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)计算:﹣12016+(﹣5)×[(﹣2)3+2]﹣(﹣4)2÷(﹣ )
)
(2)解方程:x﹣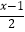 =2﹣
=2﹣ 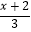
(3)已知:A= a﹣2(a﹣
a﹣2(a﹣  b2),B=﹣
b2),B=﹣  a+
a+  b2 , 且|a+2|+(b﹣3)2=0,求2A﹣6B的值.
b2 , 且|a+2|+(b﹣3)2=0,求2A﹣6B的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏东33°方向,同时又位于B船的北偏东78°方向.
(1)求∠ABC的度数;
(2)A船以每小时30海里的速度前去救援,问多长时间能到出事地点.(结果精确到0.01小时).
(参考数据:
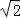 ≈1.414,
≈1.414,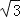 ≈1.732)
≈1.732)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市一月份的营业额为10万元,一至三月份的总营业额为45万元,若平均每月的增长率为x,则依题意列方程为( )
A. 10(1+x)2=45B. 10+10×2x=45
C. 10+10×3x=45D. 10[1+(1+x)+(1+x)2]=45
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.在同一年出生的400人中至少有两人的生日相同
B.投掷一粒骰子,连投两次点数相同的概率与连投两次点数都为1的概率是相等的
C.从一副完整的扑克牌中随机抽取一张牌恰好是红桃K,这是必然事件
D.一个袋中装有3个红球,5个白球,任意摸出一个球是红球的概率是
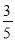
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正五边形ABCDE中,对角线AD,AC与EB分别交于点M,N,则下列结论正确的是( )
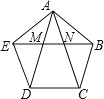
A.EM:AE=2:(
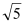 -1)
-1) B.MN:EM=(
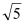 -1):(3-
-1):(3-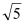 )
)C.AM:MN=(3-
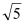 ):(
):(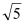 -1)
-1) D.MN:DC=(3-
 ):2
):2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,AD=6,点F是AB的中点,E为BC边上一点,且EF⊥ED,连结DF,M为DF的中点,连结MA,ME.若AM⊥ME,则AE的长为( )
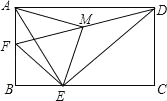
A.5 B.2
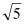 C.2
C.2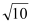 D.4
D.4
相关试题

