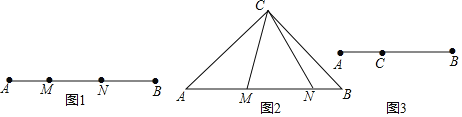
【题目】定义,如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N为线段AB的勾股分割点.
(1)已知点M,N是线段AB的勾股分割点,若AM=3,MN=5,求BN的长
(2)如图2,在Rt△ABC中,AC=BC,点M,N在斜边AB上,∠MCN=45°,求证:点M,N是线段AB的勾股分割点;阳阳在解决第(2)小题时遇到了困难,陈老师对阳阳说:要证明勾股分割点,则需设法构造直角三角形,你可以把△CBN绕点C逆时针旋转90度试试,请根据陈老师的提示完成证明过程.
(3)如图3,C是线段AB上的一定点,请在BC上画一点D,使C、D是线段AB的勾股分割点
(要求:完成尺规作图,保留作图痕迹,并在右侧分步写出作图步骤)
参考答案:
【答案】(1)4或![]() .(2)证明见解析,(3)作图见解析.
.(2)证明见解析,(3)作图见解析.
【解析】
(1)分两种切线利用勾股定理即可解决问题;
(2)如图,过点A作AD⊥AB,且AD=BN.只要证明△ADC≌△BNC,推出CD=CN,∠ACD=∠BCN,再证明△MDC≌△MNC,可得MD=MN,由此即可解决问题;
(3)根据定义画图即可.
(1)解:当MN最长时,BN=![]() =4;
=4;
当BN最长时,BN=![]() ;
;
(2)证明:如图,过点A作AD⊥AB,且AD=BN
∵AD=BN,∠DAC=∠B=45°,AC=BC,
∴△ADC≌△BNC,
∴CD=CN,∠ACD=∠BCN,
∵∠MCN=45°,
∴∠DCA+∠ACM=∠ACM+∠BCN=45°
∴∠MCD=∠BCM,
∴△MDC≌△MNC,
∴MD=MN
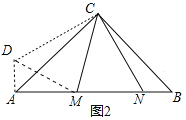
在Rt△MDA中,AD2+AM2=DM2,
∴BN2+AM2=MN2,
∴点M,N是线段AB的勾股分割点.
(3)作法:①在AB上截取CE=CA;
②作AE的垂直平分线,并截取CF=CA;
③连接BF,并作BF的垂直平分线,交AB于D;
点D即为所求;如图3中所示.
-
科目: 来源: 题型:
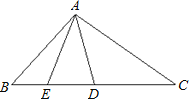
查看答案和解析>>【题目】已知:如图,D是△ABC的边BC上的一点,且CD=AB,∠BDA=∠BAD,AE是△ABD的中线.
⑴若∠B=60°,求∠C的值;
⑵求证:AD是∠EAC的平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有(写出所有正确结论的序号)
①△CMP∽△BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为2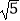 ;
;
⑤当△ABP≌△ADN时,BP=4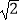 ﹣4.
﹣4.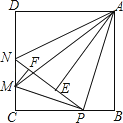
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,O为AC中点,EF过点O且EF⊥AC分别交DC于点F,交AB于点E,点G是AE中点且∠AOG=30°,给出以下结论: ①∠AFC=120°;
②△AEF是等边三角形;
③AC=3OG;
④S△AOG= S△ABC
S△ABC
其中正确的是 . (把所有正确结论的序号都选上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
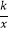 (x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.,则下列结论正确的是(将正确的结论填在横线上).
(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.,则下列结论正确的是(将正确的结论填在横线上).
①s△OEB=s△ODB , ②BD=4AD,③连接MD,S△ODM=2S△OCE , ④连接ED,则△BED∽△BCA.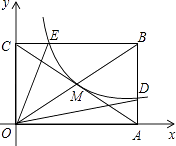
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为6,B是数轴上一点,且AB=10,动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,
(1)写出数轴上点B所表示的数 ;
(2)点P所表示的数 ;(用含t的代数式表示);
(3)M是AP的中点,N为PB的中点,点P在运动的过程中,线段MN的长度是否发生变化?若变化,说明理由;若不变,请你画出图形,并求出线段MN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(﹣1,0),B(0,﹣
 ),C(2,0),其对称轴与x轴交于点D
),C(2,0),其对称轴与x轴交于点D
(1)求二次函数的表达式及其顶点坐标;
(2)若P为y轴上的一个动点,连接PD,则 PB+PD的最小值为;
PB+PD的最小值为;
(3)M(x,t)为抛物线对称轴上一动点
①若平面内存在点N,使得以A,B,M,N为顶点的四边形为菱形,则这样的点N共有 个;
②连接MA,MB,若∠AMB不小于60°,求t的取值范围.
相关试题

