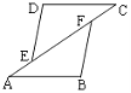
【题目】已知如图,A、E、F、C四点共线,BF=DE,AB=CD.
(1)请你添加一个条件,使△DEC≌△BFA;
(2)在(1)的基础上,求证:DE∥BF.
参考答案:
【答案】(1)添加的条件为:AE=CF(答案不唯一);(2)证明见解析;
【解析】
(1)添加的条件AE=CF,因此可得AF=CE,即可证明△DEC≌△BFA;
(2) 由(1)知△DEC≌△BFA,得到∠DEC=∠BFA,根据直线平行的判定,即可证明;
解:(1)添加的条件为:AE=CF,
证明:∵AE=CF,
∴AE+EF=CF+EF,
即:AF=CE,
又∵BF=DE,AB=CD,
∴在△DEC和△BFA中,
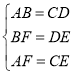
∴△DEC≌△BFA(SSS);
(2)由(1)知△DEC≌△BFA,
∴∠DEC=∠BFA
(全等三角形对应角相等),
∴DE∥BF(内错角相等,两直线平行).
-
科目: 来源: 题型:
查看答案和解析>>【题目】港珠澳大桥是世界最长的跨海大桥,连接香港大屿山、澳门半岛和广东省珠海市,其中珠海站到香港站全长约55千米,2018年10月24日上午9时正式通车.一辆观光巴士自珠海站出发,25分钟后,一辆小汽车从同一地点出发,结果同时到达香港站.已知小汽车的速度是观光巴士的1.6倍,求观光巴士的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列式子:
0×2+1=12……①
1×3+1=22……②
2×4+1=32……③
3×5+1=42……④
……
(1)第⑤个式子 ,第⑩个式子 ;
(2)请用含n(n为正整数)的式子表示上述的规律,并证明:
(3)求值:(1+
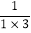 )(1+
)(1+ )(1+
)(1+ )(1+
)(1+ )…(1+
)…(1+ ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图表示玲玲骑自行车离家的距离与时间的关系.她9点离开家,15点回到家,请根据图象回答下列问题:

(1)玲玲到达离家最远的地方是什么时间?她离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)第一次休息时,她离家多远?
(4)11点~12点她骑车前进了多少千米?
-
科目: 来源: 题型:
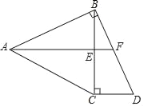
查看答案和解析>>【题目】如图,在等腰△ABC中,AB=AC,过点B作BD⊥AB,过点C作CD⊥BC,两线相交于点D,AF平分∠BAC交BC于点E,交BD于点F.
(1)若∠BAC=68°,求∠DBC;
(2)求证:点F为BD中点;
(3)若AC=BD,且CD=3,求四边形ABDC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:BD平分∠ABC,∠ABD=∠ADB,∠ABC=50°,请问:
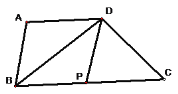
(1)∠BDC+∠C 的度数是多少?并说明理由.
(2)若P点是BC上的一动点(B点除外),∠BDP与∠BPD之和是一个确定的值吗?如果是,求出这个确定的值.如果不是,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图a是一个长为2 m、宽为2 n的长方形, 沿图中虚线用剪刀均分成四块小长方形, 然后按图b的形状拼成一个正方形。
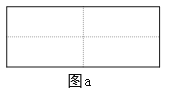

(1)你认为图b中的阴影部分的正方形的边长等于__________________。
(2)请用两种不同的方法求图b中阴影部分的面积。
方法1:___________________________ 方法2:___________________________
(3)观察图b,你能写出下列三个代数式之间的等量关系吗?
代数式: (m+n)2 ,(m-n)2,mn
_______________________________________________________
(4)根据(3)题中的等量关系,解决如下问题:
若a+b=7,ab=5,求(a-b)2的值。
相关试题

