【题目】(本题满分10分)已知四边形ABCD是矩形,对角线AC和BD相交于点P,若在矩形的上方加一个△DEA,且使DE∥AC,AE∥BD.
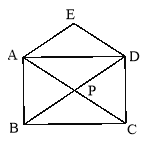
(1)求证:四边形DEAP是菱形;
(2)若AE=CD,求∠DPC的度数.
参考答案:
【答案】(1)见解析;(2)∠DPC=60°.
【解析】
试题(1)由题中由已知条件可得其为平行四边形,再加上一组邻边相等即为菱形.
(2)由(1)中的结论即可证明△PDC为等边三角形,从而得出∠DPC=60°.
试题解析:(1)∵DE∥AC,AE∥BD,
∴四边形DEAP为平行四边形,
∵ABCD为矩形,
∴AP=![]() AC,DP=
AC,DP=![]() BD,AC=BD,
BD,AC=BD,
∴AP=PD,PD=CP,
∴四边形DEAP为菱形;
∵四边形DEAP为菱形,
∴AE=PD,
∵AE=CD,
∴PD=CD,
∵PD=CP(上小题已证),
∴△PDC为等边三角形,
∴∠DPC=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O交BC,AC于D,E两点,过点D作⊙O的切线,交AC于点F,交AB的延长线于点G.
(1)求证:EF=CF;
(2)若cos∠ABC=
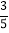 ,AB=10,求线段AF的长.
,AB=10,求线段AF的长.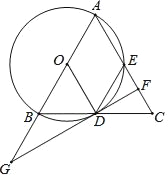
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是ts(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:四边形AEFD是平行四边形;
(2)当t为何值时,△DEF为直角三角形?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点E的坐标_____.
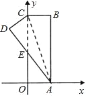
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+b与坐标轴交于A,B两点,其中点B的坐标为(0,4),tan∠BAO=
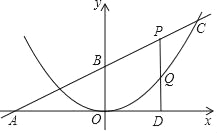
 ,一条抛物线的顶点为坐标原点,且与直线y=kx+b交于点C(m,8),点P为线段BC上一动点(不与点B,点C重合),PD⊥x轴于点D,交抛物线于点Q.
,一条抛物线的顶点为坐标原点,且与直线y=kx+b交于点C(m,8),点P为线段BC上一动点(不与点B,点C重合),PD⊥x轴于点D,交抛物线于点Q.(1)求直线和抛物线的函数关系式;
(2)设点P的横坐标为t,线段PQ的长度为d,求出d与t之间的函数关系式,并求出d的最大值;
(3)是否存在点P的位置,使得以点P,D,B为顶点的三角形是等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并解决后面的问题.
材料:一般地,
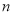 个相同的因数
个相同的因数 相乘:
相乘: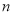 个
个 记为
记为 ,如
,如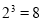 ,此时,3叫做以2为底8的对数,记为
,此时,3叫做以2为底8的对数,记为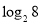 (即
(即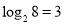 ).
).一般地,若
 (
(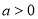 且
且 ,
,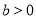 ),则
),则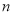 叫做以
叫做以 为底
为底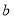 的对数,记为
的对数,记为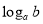 (即
(即 ).如
).如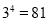 ,则4叫做以3为底81的对数,记为
,则4叫做以3为底81的对数,记为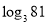 (即
(即 ).
).问题:(1)计算以下各对数的值:
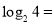 ________,
________, ________,
________, ________.
________.(2)观察(1)中三数4、16、64之间满足怎样的关系式?
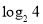 、
、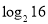 、
、 之间又满足怎样的关系式?______________________________________________________________________________
之间又满足怎样的关系式?______________________________________________________________________________(3)由(2)的结果,你能归纳出一个一般性的结论吗?
 ____________________(
____________________(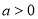 且
且 ,
,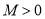 ,
, )
)(4)根据幂的运算法则:
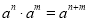 以及对数的含义证明(3)中结论.
以及对数的含义证明(3)中结论.
相关试题

