【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是ts(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:四边形AEFD是平行四边形;
(2)当t为何值时,△DEF为直角三角形?请说明理由.

参考答案:
【答案】(1)见解析;(2)当t=![]() 或12时,△DEF为直角三角形.
或12时,△DEF为直角三角形.
【解析】
(1)根据三角形内角和定理得到∠C=30°,根据直角三角形的性质求出DF,得到DF=AE,根据平行四边形的判定定理证明;
(2)分∠EDF=90°、∠DEF=90°两种情况,根据直角三角形的性质列出算式,计算即可.
(1)∵∠B=90°,∠A=60°,
∴∠C=30°,
∴AB=![]() AC=30,
AC=30,
由题意得,CD=4t,AE=2t,
∵DF⊥BC,∠C=30°,
∴DF=![]() CD=2t,
CD=2t,
∴DF=AE,
∵DF∥AE,DF=AE,
∴四边形AEFD是平行四边形;
(2)当∠EDF=90°时,如图①,
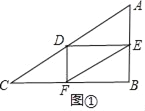
∵DE∥BC,
∴∠ADE=∠C=30°,
∴AD=2AE,即60﹣4t=2t×2,
解得,t=![]() ,
,
当∠DEF=90°时,如图②,

∵AD∥EF,
∴DE⊥AC,
∴AE=2AD,即2t=2×(60﹣4t),
解得,t=12,
综上所述,当t=![]() 或12时,△DEF为直角三角形.
或12时,△DEF为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点E、F分别在直线AB、CD上,点G、H在两直线之间,线段EF与GH相交于点O,且有∠AEF+∠CFE=180°,∠AEF﹣∠1=∠2,则在图中相等的角共有( )

A. 5对B. 6对C. 7对D. 8对
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点
 与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两名运动员进行射击选拨赛,每人射击10次,其中射击中靶情况如下表:
第一次
第二次
第三次
第四次
第五次
第六次
第七次
第八次
第九次
第十次
甲
7
10
8
10
9
9
10
8
10
9
乙
10
7
10
9
9
10
8
10
7
10
(1)选手甲的成绩的中位数是__________分;选手乙的成绩的众数是__________分;
(2)计算选手甲的平均成绩和方差;
(2)已知选手乙的成绩的方差是1.4,则成绩较稳定的是哪位选手?(直按写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
 经过点A(﹣3,0)和点B(2,0).直线
经过点A(﹣3,0)和点B(2,0).直线 (
( 为常数,且
为常数,且 )与BC交于点D,与
)与BC交于点D,与 轴交于点E,与AC交于点F.
轴交于点E,与AC交于点F.(1)求抛物线的解析式;
(2)连接AE,求
 为何值时,△AEF的面积最大;
为何值时,△AEF的面积最大;(3)已知一定点M(﹣2,0).问:是否存在这样的直线
 ,使△BDM是等腰三角形?若存在,请求出
,使△BDM是等腰三角形?若存在,请求出 的值和点D的坐标;若不存在,请说明理由.
的值和点D的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为奖励优秀学生,某校准备购买一批文具袋和圆规作为奖品,已知购买1个文具袋和2个圆规需21元,购买2个文具袋和3个圆规需39元。
(1)求文具袋和圆规的单价。
(2)学校准备购买文具袋20个,圆规若干,文具店给出两种优惠方案:
方案一:购买一个文具袋还送1个圆规。
方案二:购买圆规10个以上时,超出10个的部分按原价的八折优惠,文具袋不打折.
①设购买面规m个,则选择方案一的总费用为______,选择方案二的总费用为______.
②若学校购买圆规100个,则选择哪种方案更合算?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①b+2a=0;②abc>0;③a﹣2b+4c<0;④8a+c>0.其中正确的有( )个.
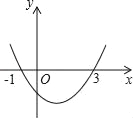
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

