Question

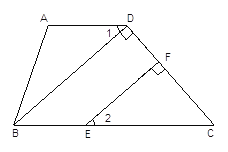
【题目】如图，在四边形ABCD中，∠A=104°－∠2，∠ABC=76°＋∠2，BD⊥CD于D，EF⊥CD于F．

求证：∠1=∠2．请你完成下面证明过程．

证明：因为∠A＝104°－∠2，∠ABC＝76°＋∠2，（ ）

所以 ∠A＋∠ABC＝104°－∠2＋76°＋∠2， （ 等式性质 ）

即 ∠A＋∠ABC＝180°

所以 AD∥BC，（ ）

所以 ∠1＝∠DBC，（ ）

因为 BD⊥DC，EF⊥DC，（ ）

所以 ∠BDC=90°,∠EFC=90°,( )

所以 ∠BDC=∠EFC,

所以 BD∥ ，（ ）

所以 ∠2＝∠DBC，（ ）

所以 ∠1＝∠2 （ ）．

Answer 1

【答案】见解析.

【解析】首先观察已知条件中的角，不难发现：两个角互补，得平行．再根据平行线的性质得到有关角之间的关系，运用等量代换的方法证明最后的结论．

证明：因为∠A＝104°－∠2，∠ABC＝76°＋∠2，（已知 ）

所以∠A＋∠ABC＝104°－∠2＋76°＋∠2， （ 等式性质 ）

即 ∠A＋∠ABC＝180°

所以 AD∥BC，（同旁内角互补，两直线平行）

所以 ∠1＝∠DBC，（两直线平行，内错角相等）

因为 BD⊥DC，EF⊥DC，（已知）

所以 ∠BDC=90°,∠EFC=90°,( 垂直定义)

所以 ∠BDC=∠EFC,

所以 BD∥EF，（同位角相等，两直线平行）

所以 ∠2＝∠DBC，（两直线平行，同位角相等）

所以 ∠1＝∠2 （等量代换）．