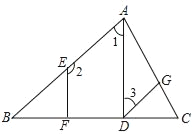
【题目】如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°,试说明:∠GDC=∠B.请补充说明过程,并在括号内填上相应的理由.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90° ,
∴EF∥AD( ),
∴ +∠2=180°( ).
又∵∠2+∠3=180°(已知),
∴∠1=∠3( ),
∴AB∥ ( ),
∴∠GDC=∠B( ).
参考答案:
【答案】见解析
【解析】
求出AD∥EF,根据平行线的性质得出∠2+∠1=180°,求出∠1=∠3,根据平行线的判定得出DG∥AB,根据平行线的性质得出∠GDC=∠B即可.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB =90°( 垂直的定义 ),
∴EF∥AD (同位角相等,两直线平行),
∴ ∠1 +∠2=180°(两直线平行,同旁内角互补).
又∵∠2+∠3=180°(已知),
∴∠1=∠3 (同角的补角相等),
∴AB∥ DG (内错角相等,两直线平行),
∴∠GDC=∠B ( 两直线平行,同位角相等 ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,O是等边△ABC内一点,连接OA、OB、OC,且OA=3,OB=4,OC=5,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.求:

①旋转角的度数;
②线段OD的长;
③∠BDC的度数.
(2)如图2所示,O是等腰直角△ABC(∠ABC=90°)内一点,连接OA、OB、OC,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.当OA、OB、OC满足什么条件时,∠ODC=90°?请给出证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明元旦前到文具超市用15元买了若干练习本,元旦这一天,该超市开展优惠活动,同样的练习本比元旦前便宜0.2元,小明又用20.7元钱买练习本,所买练习本的数量比上一次多50%,小明元旦前在该超市买了多少本练习本?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
(1)根据图示填写下表:
平均数/分
中位数/分
众数/分
A校
______
85
______
B校
85
______
100
(2)结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
(3)计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.

-
科目: 来源: 题型:
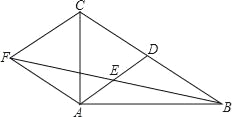
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)试判断四边形ADCF的形状,并证明;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D.若BC=16,CD=6,则AC=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一自助夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了200m到达B地,再沿北偏东30°方向走,恰能到达目的地C(如图),那么,由此可知,B、C两地相距 m.
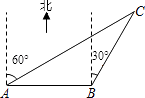
相关试题

