【题目】如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.

(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
参考答案:
【答案】(1)证明见解析;(2)△AOD是直角三角形.理由见解析;(3)125°,或110°,或140°.
【解析】
试题分析:此题有一定的开放性,要找到变化中的不变量才能有效解决问题.
试题解析:(1)∵CO=CD,∠OCD=60°,
∴△COD是等边三角形;
(2)当α=150°,即∠BOC=150°时,△AOD是直角三角形.
∵△BOC≌△ADC,
∴∠ADC=∠BOC=150°,
又∵△COD是等边三角形,
∴∠ODC=60°,
∴∠ADO=90°,
即△AOD是直角三角形;
(3)①要使AO=AD,需∠AOD=∠ADO.
∵∠AOD=360°-∠AOB-∠COD-α=360°-110°-60°-α=190°-α,∠ADO=α-60°,
∴190°-α=α-60°
∴α=125°;
②要使OA=OD,需∠OAD=∠ADO.
∵∠AOD=190°-α,∠ADO=α-60°,
∴∠OAD=180°-(∠AOD+∠ADO)=50°,
∴α-60°=50°
∴α=110°;
③要使OD=AD,需∠OAD=∠AOD.
∵190°-α=50°
∴α=140°.
综上所述:当α的度数为125°,或110°,或140°时,△AOD是等腰三角形.
-
科目: 来源: 题型:
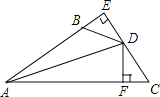
查看答案和解析>>【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求证:AD平分∠BAC;
(2)已知AC=20,AB=12,求CF的长.
-
科目: 来源: 题型:
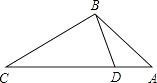
查看答案和解析>>【题目】如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )
A.∠ABD=∠C
B.∠ADB=∠ABC
C.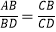
D.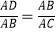
-
科目: 来源: 题型:
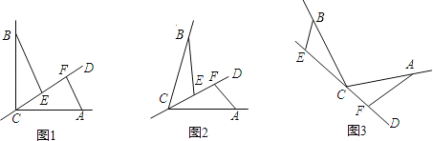
查看答案和解析>>【题目】CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE_____CF;EF_____|BE﹣AF|(填“>”,“<”或“=”);
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件_____,使①中的两个结论仍然成立。
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想并给出理由。.
-
科目: 来源: 题型:
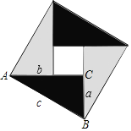
查看答案和解析>>【题目】现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若AC=b,BC=a,请你利用这个图形解决下列问题:
(1)试说明a2+b2=c2;
(2)如果大正方形的面积是6,小正方形的面积是2,求(a+b)2的值.
-
科目: 来源: 题型:
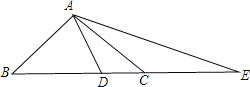
查看答案和解析>>【题目】(1)如图,在在△ABC中,已知∠BAC=900,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,CE=CA,求∠DAE的度数;
(2)如果把(1)中的“AB=AC”条件去掉,其余条件不变,那么∠DAE的度数改变吗?为什么?
(3)如果把(1)中的“∠BAC=900”改成“∠BAC>900”其余条件不变,试探究∠DAE与∠BAC的数量关系式,试证明.
-
科目: 来源: 题型:
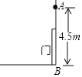
查看答案和解析>>【题目】如图,有一个由传感器A控制的灯,要装在门上方离地面4.5m的墙上,任何东西只要移至该灯5m及5m内,灯就会自动发光,小明身高1.5m,他走到离墙_______的地方灯刚好发光.
相关试题

