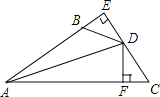
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求证:AD平分∠BAC;
(2)已知AC=20,AB=12,求CF的长.
参考答案:
【答案】(1) 见解析;(2)4.
【解析】
(1)求出∠E=∠DFC=90°,根据全等三角形的判定定理得出Rt△BED≌Rt△CFD,推出DE=DF,根据角平分线性质得出即可;
(2)根据全等三角形的性质得出AE=AF,BE=CF,即可求出答案.
(1) 证明:∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°,
∴在Rt△BED和Rt△CFD中
![]()
∴Rt△BED≌Rt△CFD(HL),
∴DE=DF,
∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC;
(2)∵Rt△BED≌Rt△CFD,
∴CF=BE,易证Rt△AED≌Rt△AFD,
∴AE=AF
设CF=BE=x,20-x=12+x
x=4,
∴CF=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,BC=2AD,点F、G分别是边BC、CD的中点,连接AF、FG,过点D作DE∥FG交AF于点E.
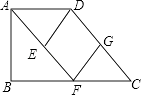
(1)求证:△AED≌△CGF;
(2)若梯形ABCD为直角梯形,∠B=90°,判断四边形DEFG是什么特殊四边形?并证明你的结论;
(3)若梯形ABCD的面积为a(平方单位),则四边形DEFG的面积为(平方单位).(只写结果,不必说理) -
科目: 来源: 题型:
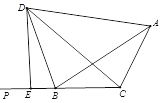
查看答案和解析>>【题目】如图,BD是△ABC的外角∠ABP的角平分线,DA=DC,DE⊥BP于点E,若AB=5,BC=3,则BE的长为 _____________
-
科目: 来源: 题型:
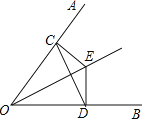
查看答案和解析>>【题目】如图,已知E是∠AOB的平分线上的一点,EC⊥OA,ED⊥OB,垂足分别是C,D.求证:OE垂直平分CD.
-
科目: 来源: 题型:
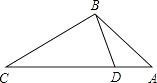
查看答案和解析>>【题目】如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )
A.∠ABD=∠C
B.∠ADB=∠ABC
C.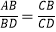
D.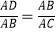
-
科目: 来源: 题型:
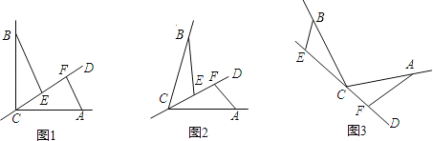
查看答案和解析>>【题目】CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE_____CF;EF_____|BE﹣AF|(填“>”,“<”或“=”);
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件_____,使①中的两个结论仍然成立。
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想并给出理由。.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.

(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
相关试题

