【题目】如图,已知直线![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的度数;
的度数;
(2)若![]() 是
是![]() 的平分线,那么
的平分线,那么![]() 是
是![]() 的平分线吗?说明你的理由.
的平分线吗?说明你的理由.
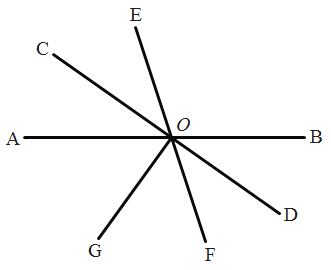
参考答案:
【答案】(1)∠AOG =54°;(2) OC是∠AOE的平分线,理由见解析.
【解析】
(1)根据A,O,B在同一直线即可求出∠AOG的度数;
(2)根据OG平分∠AOF知,∠AOF的度数,再由OG⊥CD,得∠COG=90°,即可求出∠AOE与∠AOC的度数,即可进行求证.
(1)由OG⊥CD,得∠DOG=90°,
∴∠AOG=180°-∠DOG-∠BOD=54°;
(2) OC是∠AOE的平分线,理由如下.
∵OG平分∠AOF,
∴∠AOF=2∠AOG=108°,
则∠AOE=180°-∠AOF=72°,
又∵OG⊥CD,
∴∠COG=90°,
∴∠AOC=90°-∠AOG=36°,
故∠AOE=2∠AOC,
故OC是∠AOE的平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面内有四个点A,B,C,D. 根据下列语句画图:
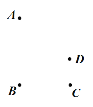
①画直线BC;
②画射线AD交直线
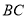 于点E;
于点E;③连接BD,用圆规在线段BD的延长线上截取DF=BD;
④在图中确定点O,使点O到点A,B,C,D的距离之和最小.
(友情提醒:截取用圆规,并保留痕迹;画完图要下结论)
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上有
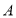 ,
, ,
,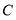 三点,给出如下定义:若其中一个点与其它两个点的距离恰好满足2倍的数量关系,则称该点是其它两个点的“关联点”.例如数轴上点
三点,给出如下定义:若其中一个点与其它两个点的距离恰好满足2倍的数量关系,则称该点是其它两个点的“关联点”.例如数轴上点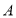 ,
, ,
,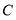 所表示的数分别为1, 3,4,此时点
所表示的数分别为1, 3,4,此时点 是点
是点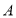 ,
,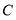 的“关联点”.
的“关联点”.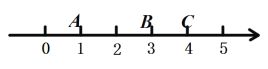
(1)若点
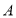 表示数-2,点
表示数-2,点 表示数1,下列各数-1, 2, 4, 6所对应的点分别是
表示数1,下列各数-1, 2, 4, 6所对应的点分别是 ,
,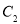 ,
,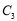 ,
,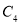 ,其中是点
,其中是点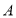 ,
, 的“关联点”的是
的“关联点”的是 (2)点
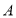 表示数-10,点
表示数-10,点 表示数15,
表示数15,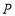 为数轴上一个动点:
为数轴上一个动点:①若点
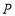 在点
在点 的左侧,且点
的左侧,且点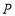 是点
是点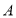 ,
, 的“关联点”,求此时点
的“关联点”,求此时点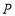 表示的数;
表示的数;②若点
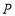 在点
在点 的右侧,点
的右侧,点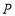 ,
,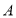 ,
, 中,有一个点恰好是其它两个点的“关联点”,请直接写出此时点
中,有一个点恰好是其它两个点的“关联点”,请直接写出此时点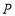 表示的数.
表示的数. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( ).
A.在一个角的内部(包括顶点)到角的两边距离相等的点的轨迹是这个角的平分线
B.到点
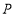 距离等于
距离等于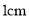 的点的轨迹是以点
的点的轨迹是以点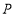 为圆心,半径长为
为圆心,半径长为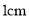 的圆
的圆C.到直线
 距离等于
距离等于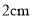 的点的轨迹是两条平行于
的点的轨迹是两条平行于 且与
且与 的距离等于
的距离等于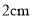 的直线
的直线D.等腰三角形
 的底边
的底边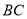 固定,顶点
固定,顶点 的轨迹是线段
的轨迹是线段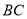 的垂直平分线
的垂直平分线 -
科目: 来源: 题型:
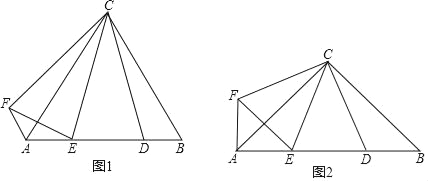
查看答案和解析>>【题目】(1)操究发现:如图1,△ABC为等边三角形,点D为AB边上的一点,∠DCE=30°,∠DCF=60°且CF=CD
①求∠EAF的度数;
②DE与EF相等吗?请说明理由
(2)类比探究:如图2,△ABC为等腰直角三角形,∠ACB=90°,点D为AB边上的一点,∠DCE=45°,CF=CD,CF⊥CD,请直接写出下列结果:
①∠EAF的度数
②线段AE,ED,DB之间的数量关系
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,MN∥EF,C为两直线之间一点.
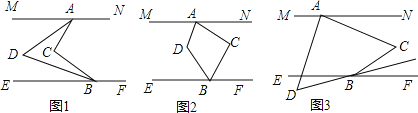
(1)如图1,若∠MAC与∠EBC的平分线相交于点D,若∠ACB=100°,求∠ADB的度数.
(2)如图2,若∠CAM与∠CBE的平分线相交于点D,∠ACB与∠ADB有何数量关系?并证明你的结论.
(3)如图3,若∠CAM的平分线与∠CBF的平分线所在的直线相交于点D,请直接写出∠ACB与∠ADB之间的数量关系: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1?

相关试题

