Question

【题目】如图1，MN∥EF，C为两直线之间一点．

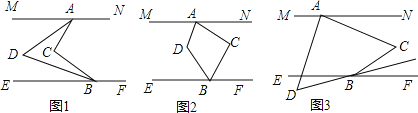
（1）如图1，若∠MAC与∠EBC的平分线相交于点D，若∠ACB=100°，求∠ADB的度数．

（2）如图2，若∠CAM与∠CBE的平分线相交于点D，∠ACB与∠ADB有何数量关系？并证明你的结论．

（3）如图3，若∠CAM的平分线与∠CBF的平分线所在的直线相交于点D，请直接写出∠ACB与∠ADB之间的数量关系： ．

Answer 1

【答案】（1）∠ADB=50°；（2）∠ADB=180°﹣∠ACB；（3）∠ADB=90°﹣ACB．

【解析】

试题分析：（1）如图1，根据平行线的性质得到∠1=∠ADH，∠2=∠BDH，∠MAC=∠ACG，∠EBC=∠BCG，根据角平分线的定义得到∠1=ACG，∠2=，即可得到结论；

（2）根据平行线的性质得到∠1=∠ADH，∠2=∠BDH，∠NAC=∠ACG，∠FBC=∠BCG，根据角平分线的定义得到∠1=ACG，∠2=，根据平角的定义即可得到结论；

（3）根据平行线的性质得到∠1=∠ADH，∠2=∠BDH，∠NAC=∠ACG，∠FBC=∠BCG，根据平行线的定义得到∠1=MAC，∠2=∠CBF，根据四边形的内角和和角的和差即可得到结论．

解：（1）如图1，过C作CG∥MN，DH∥MN，

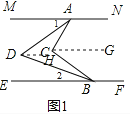
∵MN∥EF，

∴MN∥CG∥DH∥EF，

∴∠1=∠ADH，∠2=∠BDH，

∠MAC=∠ACG，∠EBC=∠BCG，

∵∠MAC与∠EBC的平分线相交于点D，

∴∠1=ACG，∠2=，

∴∠ADB=（∠ACG+∠BCG）=∠ACB；

∵∠ACB=100°，

∴∠ADB=50°；

（2）如图2，过C作CG∥MN，DH∥MN，

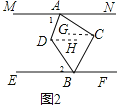
∵MN∥EF，

∴MN∥CG∥DH∥EF，

∴∠1=∠ADH，∠2=∠BDH，

∠NAC=∠ACG，∠FBC=∠BCG，

∵∠MAC与∠EBC的平分线相交于点D，

∴∠1=ACG，∠2=，

∴∠ADB=∠1+∠2=（∠MAC+∠EBC）=（180°﹣∠NAC+180°﹣∠FBC）=（360°﹣∠ACB），

∴∠ADB=180°﹣∠ACB；

（3）如图3，过C作CG∥MN，DH∥MN，

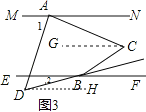
∵MN∥EF，

∴MN∥CG∥DH∥EF，

∴∠1=∠ADH，∠2=∠BDH，

∠NAC=∠ACG，∠FBC=∠BCG，

∵∠MAC与∠FBC的平分线相交于点D，

∴∠1=MAC，∠2=∠CBF，

∵∠ADB=360°﹣∠1﹣（180°﹣∠2）﹣∠ACB=360°﹣∠MAC﹣（180°﹣∠CBF）﹣∠ACB=360°﹣（180°﹣∠ACG）﹣（180°﹣∠BCG）=90°﹣∠ACB．

∴∠ADB=90°﹣ACB．

故答案为：∠ADB=90°﹣ACB．