【题目】一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.
(1)求摸出1个球是白球的概率;
(2)摸出1个球,记下颜色后放回,并搅均,再摸出1个球.求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);
(3)现再将n个白球放入布袋,搅均后,使摸出1个球是白球的概率为 ![]() .求n的值.
.求n的值.
参考答案:
【答案】
(1)解:∵一个不透明的布袋里装有3个球,其中2个红球,1个白球,
∴摸出1个球是白球的概率为 ![]()
(2)解:画树状图、列表得:

第二次 第一次 | 白 | 红1 | 红2 |
白 | 白,白 | 白,红1 | 白,红2 |
红1 | 红1,白 | 红1,红1 | 红1,红2 |
红2 | 红2,白 | 红2,红1 | 红2,红2 |
∴一共有9种等可能的结果,两次摸出的球恰好颜色不同的有4种,
∴两次摸出的球恰好颜色不同的概率为 ![]()
(3)解:由题意得: ![]() ,
,
解得:n=4.
经检验,n=4是所列方程的解,且符合题意,
∴n=4.
【解析】(1)由一个不透明的布袋里装有3个球,其中2个红球,1个白球,根据概率公式直接求解即可求得答案;(2)依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率;(3)根据概率公式列方程,解方程即可求得n的值.
【考点精析】关于本题考查的分式方程的应用和列表法与树状图法,需要了解列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位);当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某居民小区的一块宽为2a米,长为b米的长方形空地,为了美化环境,准备在这块长方形空地的四个顶点处修建一个半径为a米的扇形花台,然后在花台内种花,其余种草.
(1)请分别用含a、b的式子表示种花和种草的面积.(答案保留π)
(2)如果建造花台及种花费用每平方米需要资金100元,种草每平方米需要资金50元,那么美化这块空地共需资金多少元?(答案保留π)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=AD=2,∠A=60°,BC=
 ,CD=3.
,CD=3.(1)求∠ADC的度数;
(2)求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,过点B作⊙O的切线,交AC的延长线于点F.已知OA=3,AE=2,
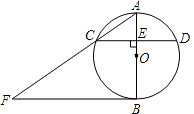
(1)求CD的长;
(2)求BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.

(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】光明中学有两块边长为x米的正方形空地,现设想按两种方式种植草皮,方式一:如图①,在正方形空地上留两条宽为2m米的路,其余种植草皮;方式二:如图②,在正方形空地四周各留一块边长为m米的正方形空地植树,其余种植草皮.学校准备两种方式都用5000元购进草皮.

(1)写出按图①,②两种方式购买草皮的单价;
(2)当x=14,m=2时,求按两种方式购买草皮的单价各是多少(结果均保留整数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(﹣2,4),过点A作AB⊥y轴,垂足为B,连接OA.
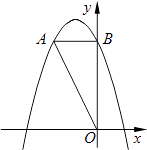
(1)求△OAB的面积;
(2)若抛物线y=﹣x2﹣2x+c经过点A.
①求c的值;
②将抛物线向下平移m个单位,使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界),求m的取值范围(直接写出答案即可).
相关试题

