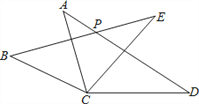
【题目】如图,在△ACD和△BCE中,AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,AD与BE相交于点P,则∠BPD的度数为 __________.
参考答案:
【答案】130
【解析】由条件可证明△ACD≌△BCE,可求得∠ACB,再利用三角形内角和可求得∠APB=∠ACB,则可求得∠BPD.
在△ACD和△BCE中,
∵AC=BC,
AD=BE,
CD=CE,
∴△ACD≌△BCE(SSS),
∴∠ACD=∠BCE,∠A=∠B,
∴∠BCA+∠ACE=∠ACE+∠ECD,
∴∠ACB=∠ECD=![]() (∠BCD-∠ACE)=
(∠BCD-∠ACE)=![]() ×(155°-55°)=50°,
×(155°-55°)=50°,
∵∠B+∠ACB=∠A+∠APB,
∴∠ABP=∠ACB=50°,
∴∠BPD=180°-50°=130°,
故答案为:130.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,CE∥BF,
A. E、F、D在一直线上,BC与AD交于点O,且OE=OF,则图中有全等三角形的对数为( )
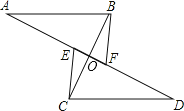
A. 2
B. 3
C. 4
D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.

(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2. -
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平整的地面上,有若干个完全相同的棱长为10cm的小正方体堆成一个几何体,如图所示.
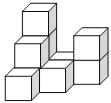
(1)这个几何体由 个小正方体组成,请画出这个几何体的三视图;
(2)如果在这个几何体的表面喷上黄色的漆,则在所有的小正方体中,有 个正方体只有一个面是黄色,有 个正方体只有两个面是黄色,有 个正方体只有三个面是黄色;
(3)若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加几个小正方体.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC和△DEF中,已知AB=DE,∠A=∠D,若要得到△ABC≌△DEF,则还要补充一个条件,在下列补充方法:①AC=DF;②∠B=∠E;③∠B=∠F;④∠C=∠F ⑤BC=EF中,则错误结论的序号是__________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:∠B=∠DEF,AB=DE,要说明△ABC≌△DEF.(1)若以“ASA”为依据,还缺条件 _________________ ;(2)若以“AAS”为依据,还缺条件___________________;(3)若以“SAS”为依据,还缺条件___________________;

相关试题

