【题目】如图,在Rt△ABC的顶点A、B在x轴上,点C在y轴上正半轴上,且
A(-1,0),B(4,0),∠ACB=90°.
(1)求过A、B、C三点的抛物线解析式;
(2)设抛物线的对称轴l与BC边交于点D,若P是对称轴l上的点,且满足以P、C、D为顶点的三角形与△AOC相似,求P点的坐标;
(3)在对称轴l和抛物线上是否分别存在点M、N,使得以A、O、M、N为顶点的四边形是平行四边形,若存在请直接写出点M、点N的坐标;若不存在,请说明理由.
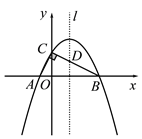
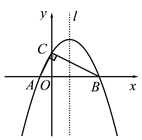
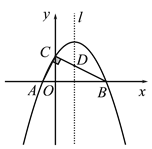
图1 备用图
参考答案:
【答案】见解析
【解析】分析:(1)根据![]() 求出点
求出点![]() 的坐标,用待定系数法即可求出抛物线的解析式.
的坐标,用待定系数法即可求出抛物线的解析式.
(2)分两种情况进行讨论即可.
(3)存在. 假设直线l上存在点M,抛物线上存在点N,使得以A、O、M、N为顶点的四边形为平行四边形.分当平行四边形![]() 是平行四边形时,当平行四边形AONM是平行四边形时,当四边形AMON为平行四边形时,三种情况进行讨论.
是平行四边形时,当平行四边形AONM是平行四边形时,当四边形AMON为平行四边形时,三种情况进行讨论.
详解:(1)易证![]() ,得
,得![]() ,
,![]()
∴OC=2,∴C(0,2),
∵抛物线过点A(-1,0),B(4,0)
因此可设抛物线的解析式为![]()
将C点(0,2)代入得:![]() ,即
,即![]()
∴抛物线的解析式为![]()
(2)如图2,
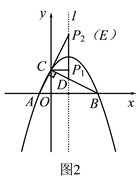
当![]() 时,
时,![]() 则P1(
则P1(![]() ,2),
,2),
当![]() 时,
时,![]()
∴OC∥l,
∴![]() ,
,
∴P2H=![]() ·OC=5,
·OC=5,
∴P2 (![]() ,5)
,5)
因此P点的坐标为(![]() ,2)或(
,2)或(![]() ,5).
,5).
(3)存在.
假设直线l上存在点M,抛物线上存在点N,使得以A、O、M、N为顶点的四边形为平行四边形.
如图3,

当平行四边形![]() 是平行四边形时,M(
是平行四边形时,M(![]() ,
,![]() ),
),![]() (
(![]() ,
,![]() ),
),
当平行四边形AONM是平行四边形时,M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() ),
),
如图4,当四边形AMON为平行四边形时,MN与OA互相平分,此时可设M(![]() ,m),则
,m),则 ![]()

∵点N在抛物线![]() 上,
上,
∴-m=-![]() ·(-
·(-![]() +1)( -
+1)( -![]() -4)=-
-4)=-![]() ,
,
∴m=![]() ,
,
此时M(![]() ,
,![]() ), N(-
), N(-![]() ,-
,-![]() ).
).
综上所述,M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() )或M(
)或M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() ) 或 M(
) 或 M(![]() ,
,![]() ), N(-
), N(-![]() ,-
,-![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分)如图,在平面直角坐标系xOy中,直线
 与y轴交于点C,与x轴交于点B,抛物线
与y轴交于点C,与x轴交于点B,抛物线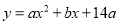 经过B、C两点,与x轴的正半轴交于另一点A,且OA :OC="2" :7.
经过B、C两点,与x轴的正半轴交于另一点A,且OA :OC="2" :7.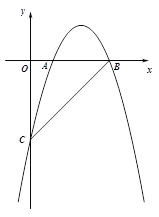


(1)求抛物线的解析式;
(2)点D为线段CB上,点P在对称轴的右侧抛物线上,PD=PB,当tan∠PDB=2,求P点的坐标;
(3)在(2)的条件下,点Q(7,m)在第四象限内,点R在对称轴的右侧抛物线上,若以点P、D、Q、R为顶点的四边形为平行四边形,求点Q、R的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两点在反比例函数y=
 的图象上,C,D两点在反比例函数y=
的图象上,C,D两点在反比例函数y=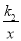 的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF=
的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF= ,则k2-k1的值为( )
,则k2-k1的值为( ) 
A. 4 B.
 C.
C. 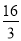 D. 6
D. 6 -
科目: 来源: 题型:
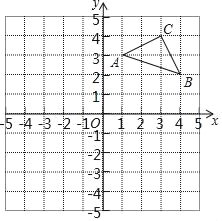
查看答案和解析>>【题目】如图,在平面直角坐标系内,已知△ABC的三个顶点坐标分别为A(1,3)、B(4,2)、C(3,4).
(1)将△ABC沿水平方向向左平移4个单位得△A1B1C1,请画出△A1B1C1;
(2)画出△ABC关于原点O成中心对称的△A2B2C2;
(3)若△A1B1C1与△A2B2C2关于点P成中心对称,则点P的坐标是
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F.
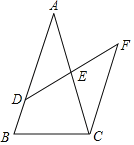
(1)证明:△ADE≌△CFE;
(2)若AB=AC,DB=2,CE=5,求CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】6月14日是“世界献血日”,某市采取自愿报名的方式组织市民义务献血.献血时要对献血者的血型进行检测,检测结果有“A型”、“B型”、“AB型”、“O型”4种类型.在献血者人群中,随机抽取了部分献血者的血型结果进行统计,并根据这个统计结果制作了两幅不完整的图表:
血型
A
B
AB
O
人数
10
5
(1)这次随机抽取的献血者人数为 人,m= ;
(2)补全上表中的数据;
(3)若这次活动中该市有3000人义务献血,请你根据抽样结果回答:
从献血者人群中任抽取一人,其血型是A型的概率是多少?并估计这3000人中大约有多少人是A型血?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点D是等腰Rt△ABC的斜边BC上一动点,连接AD,作等腰Rt△ADE,使AD=AE,且∠DAE=90°连接BE、CE.

(1)判断BD与CE的数量关系与位置关系,并进行证明;
(2)当四边形ADCE的周长最小值是6时,求BC的值.
相关试题

