【题目】(本题10分)如图,在平面直角坐标系xOy中,直线![]() 与y轴交于点C,与x轴交于点B,抛物线
与y轴交于点C,与x轴交于点B,抛物线![]() 经过B、C两点,与x轴的正半轴交于另一点A,且OA :OC="2" :7.
经过B、C两点,与x轴的正半轴交于另一点A,且OA :OC="2" :7.
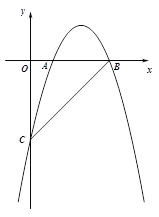


(1)求抛物线的解析式;
(2)点D为线段CB上,点P在对称轴的右侧抛物线上,PD=PB,当tan∠PDB=2,求P点的坐标;
(3)在(2)的条件下,点Q(7,m)在第四象限内,点R在对称轴的右侧抛物线上,若以点P、D、Q、R为顶点的四边形为平行四边形,求点Q、R的坐标.
参考答案:
【答案】(1)y=-![]() x2+
x2+![]() x-7 ;(2)P(8,-3);
x-7 ;(2)P(8,-3);
(3)R(10,-12),Q(7,-11)或R(6,2),Q(7,-7)
【解析】试题分析:(1)有直线解析式可以求出C点的坐标,再利用OA :OC="2" :7.求出A的坐标.最后把A、C代入抛物线解析式求出即可.
(2)先求出B的坐标可得∠OCB=∠OBC=45°,又过P作PE⊥BC于点E,所以∠CFG=∠OCB==45°就得到线段EF、BF、EP的数量关系;又tan∠PDB=2可以得到线段EP、DE、PD的数量关系,然后设出P、F的坐标利用他们的纵坐标相等即可求出点的坐标;
(3)若以点P、D、Q、R为顶点的四边形为平行四边形有两种情况:线段PD有可能是边也有可能是对角线.
当PD是边时,即DP∥QR时,∵B(7,0),Q(7,n)∴BQ∥y轴
过P作PN∥BQ,过D作DN⊥BQ交PN于点N,过R作RM⊥BQ于点M. 设PD交BQ于点T,DN交BM于点I
即可证明△RMQ≌△DNP,再求出D点的坐标,设R点的横坐标为t,∵RM=DN,∴t-7=8-5解得t=10,再把t=10带入抛物线即可求出R、Q;当PD是对角线时,同理求出.
试题解析:(1)∵直线y=kx-7与y轴的负半轴交于点C ∴C(0,-7) ∴OC=7
∵抛物线y=ax2+bx+14a经过点C,∴14a=-7,∴a =-![]() ∴y=-
∴y=-![]() x2+bx-7
x2+bx-7
∵OA :OC="2" :7.∴OA=2,∴A(2,0)∵抛物线y=-![]() x2+bx-7经过点A
x2+bx-7经过点A
∴b=![]() ∴抛物线的解析式为y=-
∴抛物线的解析式为y=-![]() x2+
x2+![]() x-7
x-7

(2)如图1,∵抛物线y=-![]() x2+
x2+![]() x-7经过B点, 令y=0解得x=7或x=2(舍)∴B(7,0)
x-7经过B点, 令y=0解得x=7或x=2(舍)∴B(7,0)
∴OB=7∴OC=OB∴∠OCB=∠OBC=45°
过点P作PF⊥x轴于点G,交CB延长线于点F,
则PF∥y轴,∴∠CFG=∠OCB==45°
∴BF=![]() GF
GF
过P作PE⊥BC于点E,
∵PD=PB
∴∠PBD=∠PDB
∴tan∠PBD=tan∠PDB=2
∴PE=2BE
∵EF=PE ∴BF=BE
∴PF=![]() PE=2
PE=2![]() BE=2
BE=2![]() BF=4GF,
BF=4GF,
∴PG="3GF"
∵直线y=kx-7过B点 ∴k=1 ∴y=x-7
设F(![]() ),则P(
),则P(![]() )
)
因为点P在抛物线y=-![]() x2+
x2+![]() x-7上,
x-7上,
所以,![]()
解得m=7(舍)或m=8
∴P(8,-3)

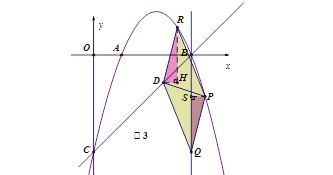
如图2,当DP∥QR时,即四边形DQRP是平行四边形 ∵B(7,0),Q(7,n)∴BQ∥y轴
过P作PN∥BQ,过D作DN⊥BQ交PN于点N,
过R作RM⊥BQ于点M.
设PD交BQ于点T,DN交BM于点I
∴∠DTB=∠DPN,∠PTQ=∠RQM, ∵∠DTB=∠PTQ
∴∠DPN=∠RQM
∵四边形DPRQ是平行四边形
∴DP=RQ
∵∠RMQ=∠DNP,∴△RMQ≌△DNP
∴RM=DN,MQ=PN
由(2)可求F(8,1),GF=1,BD=2BE=![]() BF=
BF=![]()
∵∠QBC=45°,∴BI=DI=2 ∴D(5,-2)
设R点的横坐标为t,∵RM=DN,∴t-7=8-5
解得t=10
∵点R在抛物线y=-![]() x2+
x2+![]() x-7 上,
x-7 上,
∴当t=10时,![]()
∴R(10,-12)
∵MQ=PN
∴3-2=-12-n,∴n=-11
∴R(10,-12),Q(7,-11)
如图3,当DR∥QP时,即四边形DQPR是平行四边形
同理可求得R(6,2),Q(7,-7)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,BC=6,AB=10.点Q与点B在AC的同侧,且AQ⊥AC.

(1)如图1,点Q不与点A重合,连结CQ交AB于点P.设AQ=x,AP=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(2)是否存在点Q,使△PAQ与△ABC相似,若存在,求AQ的长;若不存在,请说明理由;
(3)如图2,过点B作BD⊥AQ,垂足为D.将以点Q为圆心,QD为半径的圆记为⊙Q.若点C到⊙Q上点的距离的最小值为8,求⊙Q的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AC=BC,∠BAC的平分线AD交BC于点D,分别过点A作AE∥BC,过点B作BE∥AD,AE与BE相交于点E.若CD=2,则四边形ADBE的面积是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标为(0,6),点B在x轴的正半轴上.若点P、Q在线段AB上,且PQ为某个一边与x轴平行的矩形的对角线,则称这个矩形为点P、Q的“涵矩形”。下图为点P、Q的“涵矩形”的示意图.
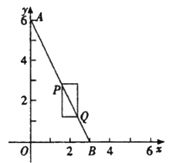
(1)点B的坐标为(3,0);
①若点P的横坐标为
 ,点Q与点B重合,则点P、Q的“涵矩形”的周长为 .
,点Q与点B重合,则点P、Q的“涵矩形”的周长为 .②若点P、Q的“涵矩形”的周长为6,点P的坐标为(1,4),则点E(2,1),F(1,2),G(4,0)中,能够成为点P、Q的“涵矩形”的顶点的是 .
(2)四边形PMQN是点P、Q的“涵矩形”,点M在△AOB的内部,且它是正方形;
①当正方形PMQN的周长为8,点P的横坐标为3时,求点Q的坐标.
②当正方形PMQN的对角线长度为/2时,连结OM.直接写出线段OM的取值范围 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两点在反比例函数y=
 的图象上,C,D两点在反比例函数y=
的图象上,C,D两点在反比例函数y=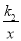 的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF=
的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF= ,则k2-k1的值为( )
,则k2-k1的值为( ) 
A. 4 B.
 C.
C. 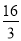 D. 6
D. 6 -
科目: 来源: 题型:
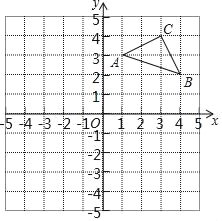
查看答案和解析>>【题目】如图,在平面直角坐标系内,已知△ABC的三个顶点坐标分别为A(1,3)、B(4,2)、C(3,4).
(1)将△ABC沿水平方向向左平移4个单位得△A1B1C1,请画出△A1B1C1;
(2)画出△ABC关于原点O成中心对称的△A2B2C2;
(3)若△A1B1C1与△A2B2C2关于点P成中心对称,则点P的坐标是
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC的顶点A、B在x轴上,点C在y轴上正半轴上,且
A(-1,0),B(4,0),∠ACB=90°.
(1)求过A、B、C三点的抛物线解析式;
(2)设抛物线的对称轴l与BC边交于点D,若P是对称轴l上的点,且满足以P、C、D为顶点的三角形与△AOC相似,求P点的坐标;
(3)在对称轴l和抛物线上是否分别存在点M、N,使得以A、O、M、N为顶点的四边形是平行四边形,若存在请直接写出点M、点N的坐标;若不存在,请说明理由.
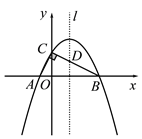
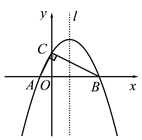
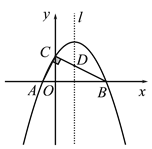
图1 备用图
相关试题

