【题目】如图所示,在△ABC中,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F.
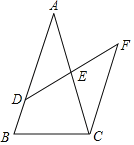
(1)证明:△ADE≌△CFE;
(2)若AB=AC,DB=2,CE=5,求CF.
参考答案:
【答案】(1)详见解析;(2)8
【解析】
(1)根据AAS或ASA证明△ADE≌△CFE即可;
(2)由AB=AC,DB=2,CE=5可得AD的长,利用全等三角形的性质求出CF=AD,即可解决问题.
解:(1)证明:∵E是边AC的中点,
∴AE=CE.
又∵CF∥AB,
∴∠A=∠ACF,∠ADF=∠F,
在△ADE与△CFE中,
∠A=∠ACF,∠ADF=∠F,AE=CE,
∴△ADE≌△CFE(AAS).
(2)∵CE=5,E是边AC的中点,
∴AE=CE=5,
∴AC=10,
∴AB=AC=10,
∴AD=AB﹣BD=10﹣2=8,
∵△ADE≌△CFE,
∴CF=AD=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两点在反比例函数y=
 的图象上,C,D两点在反比例函数y=
的图象上,C,D两点在反比例函数y=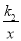 的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF=
的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF= ,则k2-k1的值为( )
,则k2-k1的值为( ) 
A. 4 B.
 C.
C. 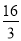 D. 6
D. 6 -
科目: 来源: 题型:
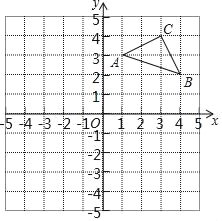
查看答案和解析>>【题目】如图,在平面直角坐标系内,已知△ABC的三个顶点坐标分别为A(1,3)、B(4,2)、C(3,4).
(1)将△ABC沿水平方向向左平移4个单位得△A1B1C1,请画出△A1B1C1;
(2)画出△ABC关于原点O成中心对称的△A2B2C2;
(3)若△A1B1C1与△A2B2C2关于点P成中心对称,则点P的坐标是
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC的顶点A、B在x轴上,点C在y轴上正半轴上,且
A(-1,0),B(4,0),∠ACB=90°.
(1)求过A、B、C三点的抛物线解析式;
(2)设抛物线的对称轴l与BC边交于点D,若P是对称轴l上的点,且满足以P、C、D为顶点的三角形与△AOC相似,求P点的坐标;
(3)在对称轴l和抛物线上是否分别存在点M、N,使得以A、O、M、N为顶点的四边形是平行四边形,若存在请直接写出点M、点N的坐标;若不存在,请说明理由.
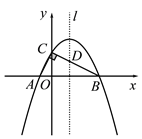
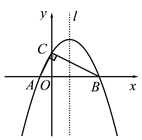
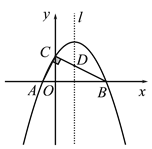
图1 备用图
-
科目: 来源: 题型:
查看答案和解析>>【题目】6月14日是“世界献血日”,某市采取自愿报名的方式组织市民义务献血.献血时要对献血者的血型进行检测,检测结果有“A型”、“B型”、“AB型”、“O型”4种类型.在献血者人群中,随机抽取了部分献血者的血型结果进行统计,并根据这个统计结果制作了两幅不完整的图表:
血型
A
B
AB
O
人数
10
5
(1)这次随机抽取的献血者人数为 人,m= ;
(2)补全上表中的数据;
(3)若这次活动中该市有3000人义务献血,请你根据抽样结果回答:
从献血者人群中任抽取一人,其血型是A型的概率是多少?并估计这3000人中大约有多少人是A型血?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点D是等腰Rt△ABC的斜边BC上一动点,连接AD,作等腰Rt△ADE,使AD=AE,且∠DAE=90°连接BE、CE.

(1)判断BD与CE的数量关系与位置关系,并进行证明;
(2)当四边形ADCE的周长最小值是6时,求BC的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数y=
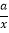 (a>0,a为常数)和y=
(a>0,a为常数)和y= 在第一象限内的图象如图所示,点M在y=
在第一象限内的图象如图所示,点M在y=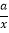 的图象上,MC⊥x轴于点C,交y=
的图象上,MC⊥x轴于点C,交y= 的图象于点A;MD⊥y轴于点D,交y=
的图象于点A;MD⊥y轴于点D,交y= 的图象于点B.当点M在y=
的图象于点B.当点M在y=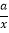 的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的个数是( )
的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的个数是( ) 
A. 0个 B. 1个 C. 2个 D. 3个
相关试题

