【题目】解下列方程
(1)2x2-4x-10=0 (用配方法)
(2)2x2+3x=4(公式法)
(3)(x-2)2=2(x-2)
(4)![]()
参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ;(3)x1=2,x2=4;(4)
;(3)x1=2,x2=4;(4)![]() ,
,![]() .
.
【解析】
(1)用配方法求解即可;
(2)用公式法求解即可;
(3)移项后用因式分解法求解即可;
(4)用公式法求解即可.
(1) ∵2x2-4x-10=0 ,
∴2x2-4x=10 ,
∴x2-2x=5 ,
∴x2-2x+1=5+1 ,
∴(x-1)2=6,
∴x-1=![]() ,
,
∴![]() ,
,![]() ;
;
(2) ∵2x2+3x=4,
∴2x2+3x-4=0,
∵a=2,b=3,c=-4,
∴=9+32=41,
∴![]() ,
,
∴![]() ,
,![]() ;
;
(3) ∵(x-2)2=2(x-2),
∴(x-2)2-2(x-2)=0,
∴(x-2) (x-2-2)=0,
∴x-2=0或x-4=0,
∴x1=2,x2=4;
(4)![]() ,
,
∵a=![]() ,b=3,c=-2
,b=3,c=-2![]() ,
,
∴=9+16=25,
∴x=![]() ,
,
∴![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y1=(m﹣2)x+2与正比例函数y2=2x图象相交于点A(2,n),一次函数y1=(m﹣2)x+2与x轴交于点B.
(1)求m、n的值;
(2)求△ABO的面积;
(3)观察图象,直接写出当x满足 时,y1>y2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC为等边三角形,点D,E为直线BC上两动点,且BD=CE. 点F,点E关于直线AC成轴对称,连接AE,顺次连接A,D,F.
(1)如图1,若点D,点E在边BC上,试判断△ADF的形状并说明理由;
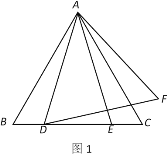
(2)如图2,若点D,点E在边BC外,求证:
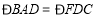 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣2x+4交x轴于点A,交y轴于点B,与反比例函数y=
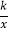 的图象有唯一的公共点C.
的图象有唯一的公共点C.(1)求k的值及C点坐标;
(2)直线l与直线y=﹣2x+4关于x轴对称,且与y轴交于点B',与双曲线y=
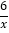 交于D、E两点,求△CDE的面积.
交于D、E两点,求△CDE的面积.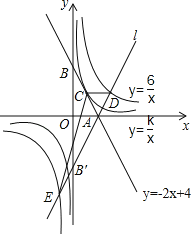
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为改善办学条件,计划采购A、B两种型号的空调,已知采购3台A型空调和2台B型空调,需费用39000元;4台A型空调比5台B型空调的费用多6000元.
(1)求A型空调和B型空调每台各需多少元;
(2)若学校计划采购A、B两种型号空调共30台,且A型空调的台数不少于B型空调的一半,两种型号空调的采购总费用不超过217000元,该校共有哪几种采购方案?
(3)在(2)的条件下,采用哪一种采购方案可使总费用最低,最低费用是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O直径,P点为半径OA上异于O点和A点的一个点,过P点作与直径AB垂直的弦CD,连接AD,作BE⊥AB,OE∥AD交BE于E点,连接AE、DE、AE交CD于F点.
(1)求证:DE为⊙O切线;
(2)若⊙O的半径为3,sin∠ADP=
 ,求AD;
,求AD;(3)请猜想PF与FD的数量关系,并加以证明.
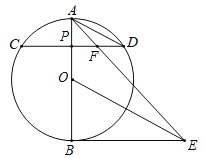
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF;其中正确的是( )
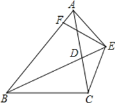
A.①②③B.①③④C.①②④D.①②③④
相关试题

