【题目】解方程:6x4-35x3+62x2-35x+6=0.
参考答案:
【答案】原方程的解为x1=2,x2=![]() ,x3=3,x4=
,x3=3,x4=![]() .
.
【解析】试题分析:本题主要考查利用整体换元法解高次方程,先将方程两边同时除以x2,得6x2-35x+62-![]() +
+![]() =0,然后分组提公因式可得: 6
=0,然后分组提公因式可得: 6![]() -35
-35![]() +62=0,此时设
+62=0,此时设
y=![]() , 则
, 则![]() =y2-2,原方程可化为: 6(y2-2)-35y+62=0,解方程求出y,然后把求出的y值代入y=
=y2-2,原方程可化为: 6(y2-2)-35y+62=0,解方程求出y,然后把求出的y值代入y=![]() ,得到关于x的方程,然后解方程即可求解.
,得到关于x的方程,然后解方程即可求解.
经验证x=0不是方程的根,原方程两边同除以x2,得6x2-35x+62-![]() +
+![]() =0,
=0,
即6![]() -35
-35![]() +62=0.
+62=0.
设y=![]() ,则
,则![]() =y2-2,
=y2-2,
原方程可变为6(y2-2)-35y+62=0.
解得y1=![]() ,y2=
,y2=![]() .
.
当![]() =
=![]() 时,解得x1=2,x2=
时,解得x1=2,x2=![]() ;
;
当![]() =
=![]() 时,解得x3=3,x4=
时,解得x3=3,x4=![]() .
.
经检验,均符合题意.
原方程的解为x1=2,x2=![]() ,x3=3,x4=
,x3=3,x4=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的面积为9πcm2 , 若圆心O到直线的距离为3cm,则直线与⊙O的位置关系是( )
A.相切
B.相交
C.相离
D.无 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx+c(a>0)的图象的顶点为D,与y轴交于点C,与x轴交于A、B两点,点A在原点的左侧,点B的坐标为(3,0),OB=OC=3OA.
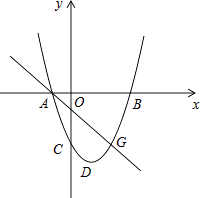
(1)求这个二次函数的解析式;
(2)如图,若点G(2,m)是该抛物线上一点,E是直线AG下方抛物线上的一动点,当点E运动到什么位置时,△AEG的面积最大?求此时点E的坐标和△AEG的最大面积;
(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】设方程4x2-7x-3=0的两根为x1,x2,不解方程求下列各式的值.
(1)(x1-3)(x2-3);(2)
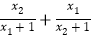 ;(3)x1-x2.
;(3)x1-x2. -
科目: 来源: 题型:
查看答案和解析>>【题目】将1,
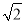 ,
, 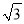 三个数按图中方式排列,若规定(a,b)表示第a排第b列的数,则(8,2)与(10,10)表示的两个数的积是( )
三个数按图中方式排列,若规定(a,b)表示第a排第b列的数,则(8,2)与(10,10)表示的两个数的积是( )
A.
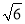 B.
B. 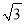 C.
C.  D. 1
D. 1 -
科目: 来源: 题型:
查看答案和解析>>【题目】食品安全是关乎民生的重要问题,在食品中添加过量的添加剂对人体健康有害,但适量的添加剂对人体健康无害而且有利于食品的储存和运输.为提高质量,做进一步研究,某饮料加工厂需生产A、B两种饮料共100瓶,需加入同种添加剂270克,其中A饮料每瓶需加添加剂2克,B饮料每瓶需加添加剂3克,饮料加工厂生产了A、B两种饮料各多少瓶?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车 间生产一批圆柱形机器零件,从中抽出了 6 件进行检验,把标准直径的长记为 0,比标准直径长的记为正数,比标准直径短的记为负数,检查记录如下:
1
2
3
4
5
6
+0.2
﹣0.3
﹣0.2
+0.3
+0.4
﹣0.1
则第_________个零件最符合标准.
相关试题

