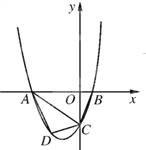
【题目】已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A, B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,过点D做x轴的垂线,交AC于点E,求线段DE的最大值.
(3)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
参考答案:
【答案】(1)y=![]() x2+
x2+![]() x-3;(2)3;(3)四边形ABCD面积有最大值
x-3;(2)3;(3)四边形ABCD面积有最大值![]() .
.
【解析】试题分析:(1)已知了B点坐标,易求得OB、OC的长,进而可将B、C的坐标代入抛物线中,求出待定系数的值,即可得出抛物线的解析式.
(2)根据A、C的坐标,易求得直线AC的解析式.可过D作x轴的垂线,交AC于E,x轴于F;易得△ADC的面积是DE与OA积的一半,可设出F点的坐标,分别代入直线AC和抛物线的解析式中,即可求出DE的长;
(3)由四边形ABCD的面积与F点横坐标间的函数关系式,根据所得函数的性质即可求出四边形ABCD的最大面积;由于AB、OC都是定值,则△ABC的面积不变,若四边形ABCD面积最大,则△ADC的面积最大.
试题解析:(1)∵B(1,0),
∴OB=1;
∵OC=3BO,
∴C(0,3);
∵y=ax2+3ax+c过B(1,0)、C(0,3),
∴![]() ;
;
解这个方程组,得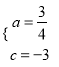 ,
,
∴抛物线的解析式为:y=![]() x2+
x2+![]() x-3;
x-3;
(2)如图:
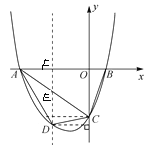
∵A(-4,0),C(0,-3),
设直线AC的解析式为y=kx+b,
代入求得:y=-![]() x-3,
x-3,
令D(x, ![]() x2+
x2+![]() x-3),E(x,-
x-3),E(x,- ![]() x-3),
x-3),
则DE=-![]() x-3-
x-3-![]() x2+
x2+![]() x-3=-
x-3=-![]() (x+2)2+3.
(x+2)2+3.
∴当x=-2时,DE有最大值3;
(3)S四边形span>ABCD=S△ABC+S△ACD=![]() +
+![]() ·DE·(AF+OF)=
·DE·(AF+OF)=![]() +2DE,
+2DE,
∴当DE取最大值3时,四边形ABCD面积有最大值![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB经过圆心O,交⊙O于A、C两点,点D在⊙O上,∠A=∠B=30°.
(1)求证:BD是⊙O的切线;
(2)若点N在⊙O上,且DN⊥AB,垂足为M,NC=10,求AD的长.
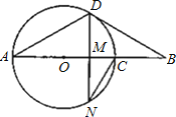
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABC 中, AB AC , BAC=100°,点 D 在 BC 上, ABD 和AFD 关于直线 AD 对称, FAC 的平分线交 BC 于点 G,连接 FG 当BAD _________.时,DFG为等腰三角形.
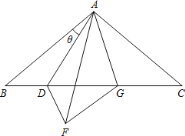
-
科目: 来源: 题型:
查看答案和解析>>【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AD是BC边上的高,∠C=30°,∠ABC=45°,BE是AC边上的中线.
(1)求证:AC=2BD;
(2)求∠CBE的度数;
(3)若点E到边BC的距离为
 ,求BC的长.
,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】6张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
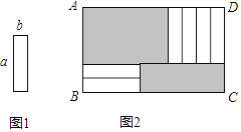
A. a=2b B. a=3b C. a=4b D. a=b
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=-2x+4与x轴y轴相交于A,B两点,点C在线段AB上,且∠COA=45°.
(1)求点A,B的坐标;
(2)求△AOC的面积;
(3)直线OC上有一动点D,过点D作直线l(不与直线AB重合)与x,y轴分别交于点E,F,当△OEF与△ABO全等时,求直线EF的解析式.
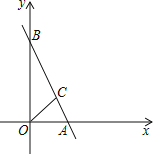
相关试题

