【题目】如图,一次函数y=-2x+4与x轴y轴相交于A,B两点,点C在线段AB上,且∠COA=45°.
(1)求点A,B的坐标;
(2)求△AOC的面积;
(3)直线OC上有一动点D,过点D作直线l(不与直线AB重合)与x,y轴分别交于点E,F,当△OEF与△ABO全等时,求直线EF的解析式.
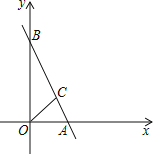
参考答案:
【答案】(1)A(2,0);B(0,4);(2)S△AOC=![]() ;(3)直线EF的解析式为y=-
;(3)直线EF的解析式为y=-![]() x+2或y=-2x-4或y=2x-4或-2x+4或y=-
x+2或y=-2x-4或y=2x-4或-2x+4或y=-![]() x-2或y=
x-2或y=![]() x-2或y=
x-2或y=![]() x+2.
x+2.
【解析】
(1)求出x=0时y的值和y=0时x的值即可得;
(2)设C(a,-2a+4),作CM⊥OA,由∠COA=45°知OM=CM,据此可得a=-2a+4,求出a的值后得出CM=OM=![]() ,再根据三角形面积公式可得答案;
,再根据三角形面积公式可得答案;
(3)分E、F在x、y轴的正半轴和负半轴的情况,依据△AOB≌△F1OE1、△AOB≌△E2OF2、△AOB≌△F3OE3得出OE、OF的长,从而得出点E和点F的坐标,再利用待定系数法求解可得.
解:(1)在直线y=-2x+4中,当x=0时y=4,
则B(0,4),
当y=0时,-2x+4=0,
解得x=2,
则A(2,0);
(2)设C(a,-2a+4),
如图1,过点C作CM⊥OA于点M,
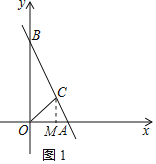
∵∠COA=45°,
∴OM=CM,
则a=-2a+4,
解得a=![]() ,
,
∴CM=OM=![]() ,
,
∴S△AOC=![]() OACM=
OACM=![]() ×2×
×2×![]() =
=![]() ;
;
(3)设直线EF解析式为y=kx+b,
如图2,
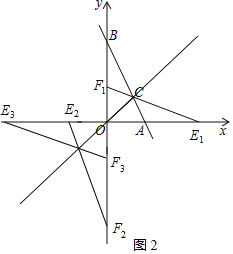
①当△AOB≌△F1OE1时,OB=OE1=4,OA=OF1=2,
则E1(4,0),F1(0,2),
代入y=kx+b得![]() ,
,
解得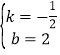 ,
,
此时直线![]() x+2,
x+2,
同理直线EF关于x轴的对称直线y=![]() x-2也符合题意;
x-2也符合题意;
②当△AOB≌△E2OF2时,OB=OF2=4,OA=OE2=2,
则E2(-2,0),F2(0,-4),
代入y=kx+b,得:![]() ,
,
解得![]()
此时直线EF解析式为y=-2x-4,
同理直线EF关于y轴的对称直线y=2x-4和关于x轴的对称直线y=-2x+4也符合要求;
③当△AOB≌△F3OE3时,OB=OE3=4,OA=OF3=2,
则E1(-4,0),F1(0,-2),
代入y=kx+b,得:![]() ,
,
解得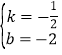 ,
,
此时直线EF解析式为y=-![]() x-2,
x-2,
同理直线EF关于x轴的对称直线y=![]() x+2也符合要求;
x+2也符合要求;
综上,直线EF的解析式为y=-![]() x+2或y=-2x-4或y=2x-4或-2x+4或y=-
x+2或y=-2x-4或y=2x-4或-2x+4或y=-![]() x-2或y=
x-2或y=![]() x-2或y=
x-2或y=![]() x+2.
x+2.
-
科目: 来源: 题型:
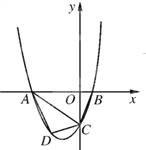
查看答案和解析>>【题目】已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A, B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,过点D做x轴的垂线,交AC于点E,求线段DE的最大值.
(3)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AD是BC边上的高,∠C=30°,∠ABC=45°,BE是AC边上的中线.
(1)求证:AC=2BD;
(2)求∠CBE的度数;
(3)若点E到边BC的距离为
 ,求BC的长.
,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】6张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
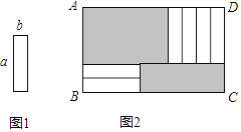
A. a=2b B. a=3b C. a=4b D. a=b
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市环保局决定购买A、B两种型号的扫地车共40辆,对城区所有公路地面进行清扫.已知1辆A型扫地车和2辆B型扫地车每周可以处理地面垃圾100吨,2辆A型扫地车和1辆B型扫地车每周可以处理垃圾110吨.
(1)求A、B两种型号的扫地车每辆每周分别可以处理垃圾多少吨?
(2)已知A型扫地车每辆价格为25万元,B型扫地车每辆价格为20万元,要想使环保局购买扫地车的资金不超过910万元,但每周处理垃圾的量又不低于1400吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少资金是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在RtABC 中, BAC 90, AB AC ,点 D 是 AB 的中点,AF CD 于 H 交 BC 于 F, BE AC 交 AF 的延长线于 E.
求证:(1)ADC ≌ BEA
(2)BC 垂直平分 DE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A、B分别在x轴、y轴上,点A与点C关于y轴对称,点E是线段AC上的点(点E不与点A、C重合)
(1)若点A的坐标为(a,0),则点C的坐标为 ;
(2)如图1,点F是线段AB上的点,若∠BEF=∠BAO,∠BAO=2∠OBE,求证:AF=CE;
(3)如图2,若点D为AC上一点,连接ED,满足BE=BD,试探究∠ABE与∠DEC的关系.

相关试题

