【题目】如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=( )

A.35° B.45° C.50° D.55°
参考答案:
【答案】D.
【解析】
试题解析:延长PF交AB的延长线于点G.

在△BGF与△CPF中,
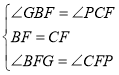 ,
,
∴△BGF≌△CPF(ASA),
∴GF=PF,
∴F为PG中点.
又∵由题可知,∠BEP=90°,
∴EF=![]() PG,
PG,
∵PF=![]() PG,
PG,
∴EF=PF,
∴∠FEP=∠EPF,
∵∠BEP=∠EPC=90°,
∴∠BEP-∠FEP=∠EPC-∠EPF,即∠BEF=∠FPC,
∵四边形ABCD为菱形,
∴AB=BC,∠ABC=180°-∠A=70°,
∵E,F分别为AB,BC的中点,
∴BE=BF,∠BEF=∠BFE=![]() (180°-70°)=55°,
(180°-70°)=55°,
∴∠FPC=55°.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2b﹣2ab+b=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】判断正误(对于真命题画“√”,对于假命题画“×”):同一平面内既不重合也不平行的两条直线一定相交.( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2(x+1)2﹣2与y轴的交点的坐标是( )
A. (0,﹣2) B. (﹣2,0) C. (0,﹣1) D. (0,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】对点P(x,y)的一次操作变换记为P1(x,y),定义其变换法则如下:P1(x,y)=(x+y,x﹣y),且规定Pn(Pn+1(x,y))(n为大于1的整数).如P1(1,2)=(3,﹣1),P2(1,2)=P1(P1(1,2))=P1(3,﹣1)=(2,4),P3(1,2)=P1(P2(1,2))=P1(2,4)=(6,﹣2),则P2016(0,﹣2)=( )
A. (0,21008) B. (0,﹣21008) C. (0,21009) D. (0,﹣21009)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC是ABCD的对角线,∠BAC=∠DAC.

(1)求证:AB=BC;
(2)若AB=2,AC=2
 ,求ABCD的面积.
,求ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在x轴正半轴上依次截取OA1=A1A2=A2A3=…=An-1An(n为正整数),过点A1、A2、A3、…、An分别作x轴的垂线,与反比例函数y=
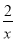 (x>0)交于点P1、P2、P3、…、Pn,连接P1P2、P2P3、…、Pn-1Pn,过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn-1An-1作垂线段,构成的一系列直角三角形(见图中阴影部分)的面积和是( )
(x>0)交于点P1、P2、P3、…、Pn,连接P1P2、P2P3、…、Pn-1Pn,过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn-1An-1作垂线段,构成的一系列直角三角形(见图中阴影部分)的面积和是( )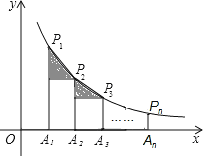
A.
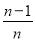 B.
B.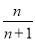 C.
C.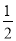 D.
D.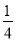
相关试题

