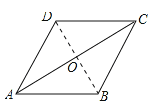
【题目】如图,AC是ABCD的对角线,∠BAC=∠DAC.

(1)求证:AB=BC;
(2)若AB=2,AC=2![]() ,求ABCD的面积.
,求ABCD的面积.
参考答案:
【答案】(1)详见解析;(2)2![]() .
.
【解析】
试题分析:(1)根据已知条件易证∠BAC=∠BCA,即可得出AB=BC;(2)连接BD交AC于O,易证四边形ABCD是菱形,根据菱形的性质可得AC⊥BD,OA=OC=![]() AC=
AC=![]() ,OB=OD=
,OB=OD=![]() BD,根据勾股定理求出OB的长,即可得BD的长,利用ABCD的面积=
BD,根据勾股定理求出OB的长,即可得BD的长,利用ABCD的面积=![]() ACBD,即可求得答案.
ACBD,即可求得答案.
试题解析:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠BCA,
∵∠BAC=∠DAC,
∴∠BAC=∠BCA,
∴AB=BC;
(2)解:连接BD交AC于O,如图所示:
∵四边形ABCD是平行四边形,AB=BC,
∴四边形ABCD是菱形,
∴AC⊥BD,OA=OC=![]() AC=
AC=![]() ,OB=OD=
,OB=OD=![]() BD,
BD,
∴OB=![]() =
=![]() =1,
=1,
∴BD=2OB=2,
∴ABCD的面积=![]() ACBD=
ACBD=![]() ×2
×2![]() ×2=2
×2=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2(x+1)2﹣2与y轴的交点的坐标是( )
A. (0,﹣2) B. (﹣2,0) C. (0,﹣1) D. (0,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=( )

A.35° B.45° C.50° D.55°
-
科目: 来源: 题型:
查看答案和解析>>【题目】对点P(x,y)的一次操作变换记为P1(x,y),定义其变换法则如下:P1(x,y)=(x+y,x﹣y),且规定Pn(Pn+1(x,y))(n为大于1的整数).如P1(1,2)=(3,﹣1),P2(1,2)=P1(P1(1,2))=P1(3,﹣1)=(2,4),P3(1,2)=P1(P2(1,2))=P1(2,4)=(6,﹣2),则P2016(0,﹣2)=( )
A. (0,21008) B. (0,﹣21008) C. (0,21009) D. (0,﹣21009)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在x轴正半轴上依次截取OA1=A1A2=A2A3=…=An-1An(n为正整数),过点A1、A2、A3、…、An分别作x轴的垂线,与反比例函数y=
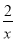 (x>0)交于点P1、P2、P3、…、Pn,连接P1P2、P2P3、…、Pn-1Pn,过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn-1An-1作垂线段,构成的一系列直角三角形(见图中阴影部分)的面积和是( )
(x>0)交于点P1、P2、P3、…、Pn,连接P1P2、P2P3、…、Pn-1Pn,过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn-1An-1作垂线段,构成的一系列直角三角形(见图中阴影部分)的面积和是( )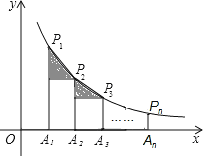
A.
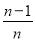 B.
B.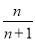 C.
C.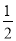 D.
D.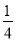
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果函数y=(m﹣2)x2+2x+3(m为常数)是二次函数,那么m取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知(ambn)3÷(ab2)2=a4b5,求m、n的值.
相关试题

