【题目】猜想归纳:为了建设经济型节约型社会,“先锋”材料厂把一批三角形废料重新利用,因此工人师傅需要把它们截成不同大小的正方形铁片.(已知:AC=40,BC=30,∠C=90°)
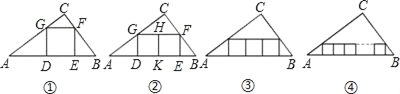
(1)如图①,若截取△ABC的内接正方形DEFG,请你求出此正方形的边长;
(2)如图②,若在△ABC内并排截取两个相同的正方形(它们组成的矩形内接于△ABC),请你求此正方形的边长;
(3)如图③,若在△ABC内并排截取三个相同的正方形(它们组成的矩形内接于△ABC),请你求此正方形的边长;
(4)猜想:如图④,假设在△ABC内并排截取n个相同的正方形,使它们组成的矩形内接于△ABC,则此正方形的边长是多少?
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() .
.
【解析】
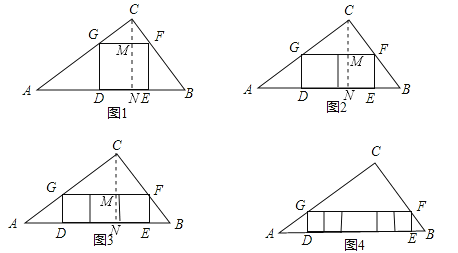
(1)根据题意画出图形,作CN⊥AB,再根据GF∥AB,可知△CGF∽△CAB,由平行得到两对同位角相等,进而得到两三角形相似,设出正方形的边长为x,根据相似三角形的性质得到比例式,进而列出关于x的方程,求出方程的解,即可求出正方形的边长;
(2)作CN⊥AB,交GF于点M,交AB于点N,同(1)可知,△CGF∽△CAB,根据对应边的比等于相似比,同理可求出正方形的边长;
(3)作CN⊥AB,交GF于点M,交AB于点N,同(1)可知,△CGF∽△CAB,根据对应边的比等于相似比,同理可求出正方形的边长;
(4)同理可得正方形的边长.
(1)在图1中作△ABC的高CN交GF于M.在Rt△ABC中,∵AC=40,BC=30,∴AB=50,CN=![]() =24.
=24.
由GF∥AB,得:△CGF∽△CAB,∴![]() .
.
设正方形的边长为x,则![]() ,解得:
,解得:![]() .
.
即正方形的边长为![]() .
.
(2)方法同(1),如图2.
△CGF∽△CAB,则![]() .
.
设小正方形的边长为x,则![]() ,解得:
,解得:![]() .
.
即小正方形的边长为![]() .
.
(3)在图3中,作CN⊥AB,交GF于点M,交AB于点N.
∵GF∥AB,∴△CGF∽△CAB,∴![]() =
=![]() ,设每个正方形的边长为x,则
,设每个正方形的边长为x,则![]() =
=![]() ,∴x=
,∴x=![]() ;
;
(4)设每个正方形的边长为x,同理得到:
则![]() =
=![]() ,则x=
,则x=![]() ,∴每个小正方形的边长为
,∴每个小正方形的边长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,直线MN与AB、CD分别交于点E、F,FG平分∠EFD,EG⊥FG于点G,若∠CFN=110°,则∠BEG=( )
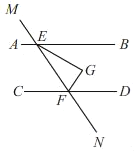
A. 20°B. 25°C. 35°D. 40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面内有一等腰Rt△ABC,∠ACB=90°,点A在直线l上.过点C作CE⊥1于点E,过点B作BF⊥l于点F,测量得CE=3,BF=2,则AF的长为( )

A. 5 B. 4 C. 8 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,△ABC中,∠A=60,BD,CE是△ABC的两条角平分线,BD,CE相交于点O,求证:BC=CD+BE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD是△ABC的中线,E是AD上的一点,且AE=2DE,连接BE并延长交AC于点F.
(1)求证:AF=FC;
(2)求
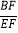 的值.
的值.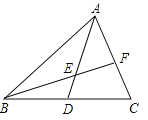
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=3 cm,BC=4 cm,动点P从点B出发以2 cm/s的速度向点C移动,动点Q从点C出发以1 cm/s的速度向点A移动,当一点到达终点时,另一点也随之停止运动.若动点P,Q同时出发,则经过多少秒时,PQ∥AB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,AB=AC,BC=8,作AD⊥BC于点D,AD=
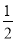 AB,点E为AC边上的中点,点P为BC上一动点,则PA+PE的最小值为_____.
AB,点E为AC边上的中点,点P为BC上一动点,则PA+PE的最小值为_____.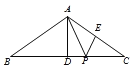
相关试题

