【题目】如图,在△ABC中,∠C=90°,AC=3 cm,BC=4 cm,动点P从点B出发以2 cm/s的速度向点C移动,动点Q从点C出发以1 cm/s的速度向点A移动,当一点到达终点时,另一点也随之停止运动.若动点P,Q同时出发,则经过多少秒时,PQ∥AB.

参考答案:
【答案】经过1.2 s时,PQ∥AB.
【解析】若PQ∥AB,Rt△ABC∽Rt△QPC,则由相似三角形性质可知,其对应边成比例,据此可得出结论.
设经过t s时,PQ∥AB,则BP=2t cm,QC=t cm,PC=(4-2t)cm.
根据题意,得Rt△ABC∽Rt△QPC,
∴![]() ,即
,即![]() ,解得:t=1.2.
,解得:t=1.2.
由于点P在BC边上的运动速度为2 cm/s,点Q在AC边上的运动速度为1 cm/s,可知t的取值范围为0<t<2,
所以t=1.2满足题目要求.
所以,经过1.2 s时,PQ∥AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,△ABC中,∠A=60,BD,CE是△ABC的两条角平分线,BD,CE相交于点O,求证:BC=CD+BE.

-
科目: 来源: 题型:
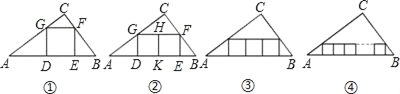
查看答案和解析>>【题目】猜想归纳:为了建设经济型节约型社会,“先锋”材料厂把一批三角形废料重新利用,因此工人师傅需要把它们截成不同大小的正方形铁片.(已知:AC=40,BC=30,∠C=90°)
(1)如图①,若截取△ABC的内接正方形DEFG,请你求出此正方形的边长;
(2)如图②,若在△ABC内并排截取两个相同的正方形(它们组成的矩形内接于△ABC),请你求此正方形的边长;
(3)如图③,若在△ABC内并排截取三个相同的正方形(它们组成的矩形内接于△ABC),请你求此正方形的边长;
(4)猜想:如图④,假设在△ABC内并排截取n个相同的正方形,使它们组成的矩形内接于△ABC,则此正方形的边长是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD是△ABC的中线,E是AD上的一点,且AE=2DE,连接BE并延长交AC于点F.
(1)求证:AF=FC;
(2)求
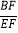 的值.
的值.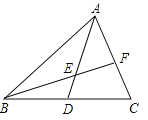
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,AB=AC,BC=8,作AD⊥BC于点D,AD=
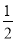 AB,点E为AC边上的中点,点P为BC上一动点,则PA+PE的最小值为_____.
AB,点E为AC边上的中点,点P为BC上一动点,则PA+PE的最小值为_____.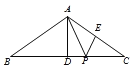
-
科目: 来源: 题型:
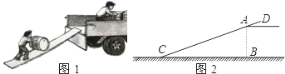
查看答案和解析>>【题目】如图1是工人将货物搬运上货车常用的方法,把一块木板斜靠在货车车厢的尾部,形成一个斜坡,货物通过斜坡进行搬运.根据经验,木板与地面的夹角为20°(即图2中∠ACB=20°)时最为合适,已知货车车厢底部到地面的距离AB=1.5m,木板超出车厢部分AD=0.5m,请求出木板CD的长度?
(参考数据:sin20°≈0.3420,cos20°≈0.9397,精确到0.1m)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里装有红、黑两种颜色的球共60只,这些球除颜色外其余完全相同.为了估计红球和黑球的个数,七(4)班的数学学习小组做了摸球实验.他们]将球搅匀后,从盒子里随机摸出一个球记下颜色,再把球放回盒子中,多次重复上述过程,得到下表中的一组统计数据:
摸球的次数n
50
100
300
500
800
1000
2000
摸到红球的次数m
14
33
95
155
241
298
602
摸到红球的频率
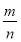
0.28
0.33
0.317
0.31
0.301
0.298
0.301
(1)请估计:当次数n足够大时,摸到红球的频率将会接近 ;(精确到0.1)
(2)假如你去摸一次,则摸到红球的概率的估计值为 ;
(3)试估算盒子里红球的数量为 个,黑球的数量为 个
相关试题

