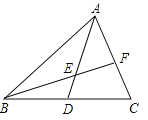
【题目】如图,已知AD是△ABC的中线,E是AD上的一点,且AE=2DE,连接BE并延长交AC于点F.
(1)求证:AF=FC;
(2)求![]() 的值.
的值.
参考答案:
【答案】(1)证明见解析;(2)3.
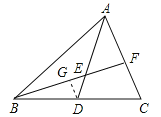
【解析】(1)过D作DG∥AC交BF于点G,则DG是△BCF的中位线,且△DEG∽△AEF,依据三角形中位线定理以及相似三角形的性质,确定AF、FC与DG的关系即可证得;
(2)根据(1)中△DEG∽△AEF,DG是△BCF的中位线,利用EF表示出BF即可.
(1)过D作DG∥AC交BF于点G.
∵DG∥AC,又AD是△ABC的中线,即BD=DC,∴DG=![]() FC.
FC.
∵DG∥AC,∴△DEG∽△AEF,∴![]() =
=![]() .又∵AE=2DE,∴
.又∵AE=2DE,∴![]() =
=![]() ,则DG=
,则DG=![]() AF,∴AF=FC;
AF,∴AF=FC;
(2)∵DG∥AC,又AD是△ABC的中线,即BD=DC,∴BF=2GF.
∵△DEG∽△AEF,∴![]() =
=![]() =
=![]() ,∴GE=
,∴GE=![]() EF,设EF=2x,则GE=x,GF=3x,∴BF=2GF=6x,则
EF,设EF=2x,则GE=x,GF=3x,∴BF=2GF=6x,则![]() =
=![]() =3.
=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面内有一等腰Rt△ABC,∠ACB=90°,点A在直线l上.过点C作CE⊥1于点E,过点B作BF⊥l于点F,测量得CE=3,BF=2,则AF的长为( )

A. 5 B. 4 C. 8 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,△ABC中,∠A=60,BD,CE是△ABC的两条角平分线,BD,CE相交于点O,求证:BC=CD+BE.

-
科目: 来源: 题型:
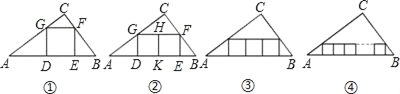
查看答案和解析>>【题目】猜想归纳:为了建设经济型节约型社会,“先锋”材料厂把一批三角形废料重新利用,因此工人师傅需要把它们截成不同大小的正方形铁片.(已知:AC=40,BC=30,∠C=90°)
(1)如图①,若截取△ABC的内接正方形DEFG,请你求出此正方形的边长;
(2)如图②,若在△ABC内并排截取两个相同的正方形(它们组成的矩形内接于△ABC),请你求此正方形的边长;
(3)如图③,若在△ABC内并排截取三个相同的正方形(它们组成的矩形内接于△ABC),请你求此正方形的边长;
(4)猜想:如图④,假设在△ABC内并排截取n个相同的正方形,使它们组成的矩形内接于△ABC,则此正方形的边长是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=3 cm,BC=4 cm,动点P从点B出发以2 cm/s的速度向点C移动,动点Q从点C出发以1 cm/s的速度向点A移动,当一点到达终点时,另一点也随之停止运动.若动点P,Q同时出发,则经过多少秒时,PQ∥AB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,AB=AC,BC=8,作AD⊥BC于点D,AD=
 AB,点E为AC边上的中点,点P为BC上一动点,则PA+PE的最小值为_____.
AB,点E为AC边上的中点,点P为BC上一动点,则PA+PE的最小值为_____.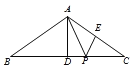
-
科目: 来源: 题型:
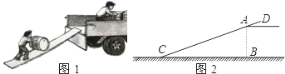
查看答案和解析>>【题目】如图1是工人将货物搬运上货车常用的方法,把一块木板斜靠在货车车厢的尾部,形成一个斜坡,货物通过斜坡进行搬运.根据经验,木板与地面的夹角为20°(即图2中∠ACB=20°)时最为合适,已知货车车厢底部到地面的距离AB=1.5m,木板超出车厢部分AD=0.5m,请求出木板CD的长度?
(参考数据:sin20°≈0.3420,cos20°≈0.9397,精确到0.1m)
相关试题

