搜索
【题目】某数学小组的10位同学站成一列做报数游戏，规则是：从前面第一位同学开始，每位同学依次报自己顺序的倒数的2倍加1，第1位同学报 
，第2位同学报 
，第3位同学报 
，…这样得到10个数的积为 ．
参考答案：
【答案】66
【解析】解：第1位同学报的数是： 
+1= 
， 第2位同学报的数是： 
+1= 
，第3位同学报的数是： 
+1= 
，第4位同学报的数是： 
+1= 
，
…，
第10为同学报的数是： 
+1= 
，∴10个数的积为 × × × ×…× = 
=66．
故答案为：66．
观察不难发现，所报的数的分数部分是分子为2，分母是连续自然数，然后都加上1，把各位同学报的数都化为假分数，然后根据有理数的乘法运算进行计算即可得解．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在直角梯形ABCD中，AD∥BC，∠B=90°，且AD=12cm，AB=8cm，DC=10cm，若动点P从A点出发，以每秒2cm的速度沿线段AD向点D运动；动点Q从C点出发以每秒3cm的速度沿CB向B点运动，当P点到达D点时，动点P、Q同时停止运动，设点P、Q同时出发，并运动了t秒，回答下列问题：
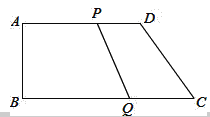
（1）BC= cm；
（2）当t为多少时，四边形PQCD成为平行四边形？
（3）当t为多少时，四边形PQCD为等腰梯形？
（4）是否存在t，使得△DQC是等腰三角形？若存在，请求出t的值；若不存在，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，E点为DF上的点，B为AC上的点，∠1=∠2，∠C=∠D．
试说明：AC∥DF．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知△ABC，求证：∠A+∠B+∠C=180°．
通过画平行线，将∠A、∠B、∠C作等角代换，使各角之和恰为一平角，依辅助线不同而得多种证法．
证法1：如图1，延长BC到D，过C画CE∥BA．
∵BA∥CE（作图2所知），
∴∠B=∠1，∠A=∠2（两直线平行，同位角、内错角相等）．
又∵∠BCD=∠BCA+∠2+∠1=180°（平角的定义），
∴∠A+∠B+∠ACB=180°（等量代换）．
如图3，过BC上任一点F，画FH∥AC，FG∥AB，这种添加辅助线的方法能证明∠A+∠B+∠C=180°吗？请你试一试．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，平行四边形ABCD的周长是26cm，对角线AC与BD相交于点O， AC⊥AB，E是BC的中点，△AOD的周长比△AOB的周长多3cm，则AE =_____cm．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，点B、E、C、F在一条直线上，AB = DF，AC = DE，BE = CF．
求证: （1） △ABC ≌ △DFE ；
（2）连接AF、BD，求证：四边形ABDF是平行四边形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，点A，B的坐标分别为A（a，0），B（n，0）且a、n满足|a+2|+
=0，现同时将点A，B分别向上平移4个单位，再向右平移3个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD．（1）求点C，D的坐标及四边形OBDC的面积；
（2）如图2，若 点P是线段BD上的一个动点，连接PC，PO，当点P在BD上移动时（不与B，D重合）
的值是否发生变化，并说明理由．（3）在四边形OBDC内是否存在一点P，连接PO，PB，PC，PD，使S△PCD=S△PBD； S△POB：S△POC=1？若存在这样一点，求出点P的坐标，若不存在，试说明理由．
相关试题
