【题目】如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.
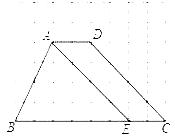
(1)在图中画出△AEF,使△AEF与△AEB关于直线AE对称,点F与点B是对称点,并求出BF的长;
(2)△AEF与四边形ABCD重叠部分的面积为 .
参考答案:
【答案】(1)作图见解析,![]() ;(2)6.
;(2)6.
【解析】
试题分析:(1)根据轴对称的性质确定出点B关于AE的对称点F即可;
(2)即DC与EF的交点为G,由四边形ADGE的面积=平行四边形ADCE的面积-△ECG的面积求解即可.
试题解析:(1)如图1所示:
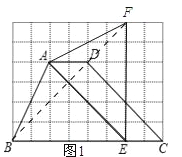
在Rt△BEF中,由勾股定理得:BF=![]() .
.
(2)如图2所示:
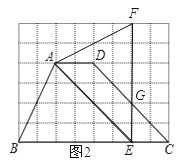
重叠部分的面积=SADEC-S△GEC
=![]() ×(2+2)×4-
×(2+2)×4-![]()
=8-2
=6.
-
科目: 来源: 题型:
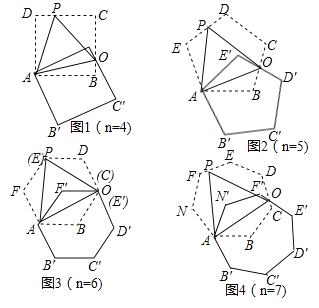
查看答案和解析>>【题目】如图,将正n边形绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为“叠弦角”,△AOP为“叠弦三角形”.
【探究证明】
(1)请在图1和图2中选择其中一个证明:“叠弦三角形”(△AOP)是等边三角形;
(2)如图2,求证:∠OAB=∠OAE′.
【归纳猜想】
(3)图1、图2中的“叠弦角”的度数分别为 , ;
(4)图n中,“叠弦三角形” 等边三角形(填“是”或“不是”)
(5)图n中,“叠弦角”的度数为 (用含n的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】六边形的内角和是( )
A.540°
B.720°
C.900°
D.360° -
科目: 来源: 题型:
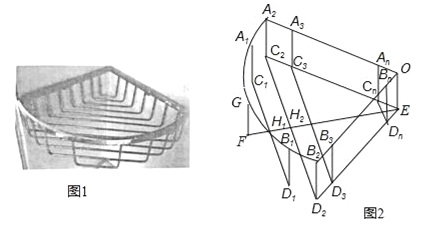
查看答案和解析>>【题目】如图1是一个用铁丝围成的篮框,我们来仿制一个类似的柱体形篮框.如图2,它是由一个半径为r、圆心角90°的扇形A2OB2,矩形A2C2EO、B2D2EO,及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、AnBnCnDn,OEFG围成,其中A1、G、B1在
 上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.
上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.(1)求d的值;
(2)问:CnDn与点E间的距离能否等于d?如果能,求出这样的n的值,如果不能,那么它们之间的距离是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h)

-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣0.5的绝对值是( )
A.0.5
B.﹣0.5
C.﹣2
D.2
相关试题

