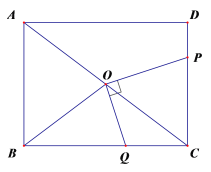
【题目】如图,在长方形ABCD中,AB=6,BC=8,点O在对角线AC上,且OA=OB=OC,点P是边CD上的一个动点,连接OP,过点O作OQ⊥OP,交BC于点Q.
(1)求OB的长度;
(2)设DP= x,CQ= y,求y与x的函数表达式(不要求写自变量的取值范围);
(3)若![]() OCQ是等腰三角形,求CQ的长度.
OCQ是等腰三角形,求CQ的长度.
参考答案:
【答案】(1)5;(2)![]() ;(3)当
;(3)当![]() 或
或![]() 时,⊿OCQ是等腰三角形.
时,⊿OCQ是等腰三角形.
【解析】
(1)利用勾股定理先求出AC的长,继而根据已知条件即可求得答案;
(2)延长QO交AD于点E,连接PE、PQ ,先证明△AEO≌△CQO,从而得OE=OQ,AE=CQ=y,由垂直平分线的性质可得PE=PQ,即![]() ,在Rt⊿EDP中,有
,在Rt⊿EDP中,有![]() ,在Rt⊿PCQ中,
,在Rt⊿PCQ中,![]() ,继而可求得答案;
,继而可求得答案;
(3)分CQ=CO,OQ=CQ,OQ=OC三种情况分别进行讨论即可求得答案.
(1)∵四边形ABCD是长方形,
∴∠ABC=90°,
∴![]() ,
,
∴OB=OA=OC=![]() ;
;
(2)延长QO交AD于点E,连接PE、PQ ,
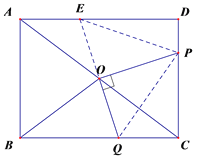
∵四边形ABCD是长方形,
∴CD=AB=6,AD=BC=8,AD//BC,
∴∠AEO=∠CQO,
在△COQ和△AOE中,
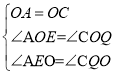 ,
,
∴△AEO≌△CQO(SAS),
∴OE=OQ,AE=CQ=y,
∴ED=AD-AE=8-y,
∵OP⊥OQ,
∴OP垂直平分EQ,
∴PE=PQ,
∴![]() ,
,
∵PD=x,
∴CP=CD-CP=6-x,
在Rt⊿EDP中,![]() ,
,
在Rt⊿PCQ中,![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)分三种情况考虑:
①如图,若CQ=CO时,此时CQ=CO=5;
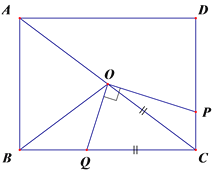
②如图,若OQ=CQ时,作OF⊥BC,垂足为点F,
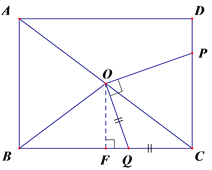
∵OB=OC,OF⊥BC,
∴BF=CF=![]() BC=4,
BC=4,
∴![]() ,
,
∵OQ=CQ,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
③若OQ=OC时,此时点Q与点B重合,点P在DC延长线上,此情况不成立,
综上所示,当![]() 或
或![]() 时,⊿OCQ是等腰三角形.
时,⊿OCQ是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点P的坐标为(1,3),把点P绕坐标原点O逆时针旋转90°后得到点Q.
(1)写出点Q的坐标是________;
(2)若把点Q向右平移
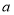 个单位长度,向下平移
个单位长度,向下平移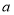 个单位长度后,得到的点
个单位长度后,得到的点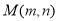 落在第四象限,求
落在第四象限,求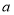 的取值范围;
的取值范围;(3)在(2)条件下,当
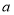 取何值,代数式
取何值,代数式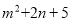 取得最小值.
取得最小值.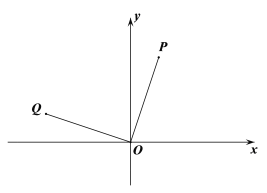
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
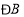 ,
,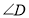 的两边分别平行.
的两边分别平行.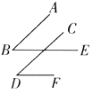
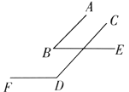
① ②
(1)在图①中,
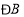 与
与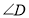 的数量关系是什么?为什么?
的数量关系是什么?为什么?(2)在图②中,
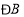 与
与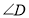 的数量关系是什么?为什么?
的数量关系是什么?为什么?(3)由(1)(2)可得结论:________;
(4)应用:若两个角的两边两两互相平行,其中一个角比另一个角的2倍少
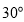 ,求这两个角的度数.
,求这两个角的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
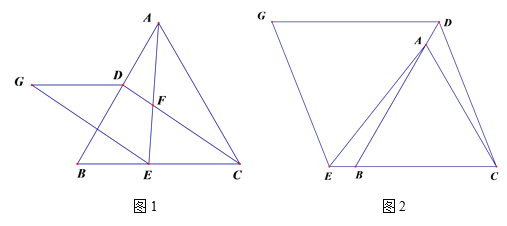
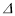 ABC为等边三角形,点D、E分别在直线AB、BC上,且AD=BE.
ABC为等边三角形,点D、E分别在直线AB、BC上,且AD=BE. (1)如图1,若点D、E分别是AB、CB边上的点,连接AE、CD交于点F,过点E作∠AEG=60°,使EG=AE,连接GD,则∠AFD= (填度数);
(2)在(1)的条件下,猜想DG与CE存在什么关系,并证明;
(3)如图2,若点D、E分别是BA、CB延长线上的点,(2)中结论是否仍然成立?请给出判断并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产480个零件.当生产任务完成一半时,停止生产进行反思和改进,用时20分钟.恢复生产后工作效率比原来可以提高20%,要求比原计划提前40分钟完成任务,那么反思改进后每小时需要生产多少个零件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】周日,小华从家沿着一条笔直的公路步行去报亭看报,看了一段时间后,他按原路返回家中,小华离家的距离y(单位:m)与他所用的时间t(单位:min)之间的函数关系如图所示,下列说法中不正确的是( )
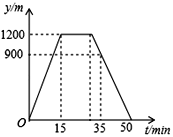
A. 小华家离报亭的距离是1200m
B. 小华从家去报亭的平均速度是80m/min
C. 小华从报亭返回家中的平均速度是80m/min
D. 小华在报亭看报用了15min
-
科目: 来源: 题型:
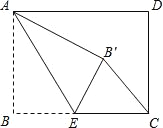
查看答案和解析>>【题目】矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为( )
A. 3 B.
 C. 2或3 D. 3或
C. 2或3 D. 3或
相关试题

