【题目】综合题
(1)如图1,若CO⊥AB,垂足为O,OE、OF分别平分∠AOC与∠BOC.求∠EOF的度数;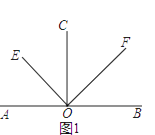
(2)如图2,若∠AOC=∠BOD=80°,OE、OF分别平分∠AOD与∠BOC.求∠EOF的度数;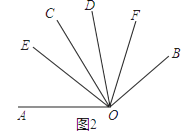
(3)若∠AOC=∠BOD=α,将∠BOD绕点O旋转,使得射线OC与射线OD的夹角为β,OE、OF分别平分∠AOD与∠BOC.若α+β≤180°,α>β,则∠EOC= . (用含α与β的代数式表示)
参考答案:
【答案】
(1)解:∵CO⊥AB,
∴∠AOC=∠BOC=90°,
∵OE平分∠AOC,
∴∠EOC= ![]() ∠AOC=
∠AOC= ![]() ×90°=45°,
×90°=45°,
∵OF平分∠BOC,
∴∠COF= ![]() ∠BOC=
∠BOC= ![]() ×90°=45°,
×90°=45°,
∠EOF=∠EOC+∠COF=45°+45°=90°;
(2)解:∵OE平分∠AOD,
∴∠EOD= ![]() ∠AOD=
∠AOD= ![]() ×(80+β)=40+
×(80+β)=40+ ![]() β,
β,
∵OF平分∠BOC,
∴∠COF= ![]() ∠BOC=
∠BOC= ![]() ×(80+β)=40+
×(80+β)=40+ ![]() β,
β,
∠COE=∠EOD﹣∠COD=40+ ![]() β﹣β=40﹣
β﹣β=40﹣ ![]() β;
β;
∠EOF=∠COE+∠COF=40﹣ ![]() β+40+
β+40+ ![]() β=80°;
β=80°;
(3)![]()
【解析】(3)如图2,∵∠AOC=∠BOD=α,∠COD=β,
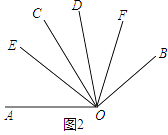
∴∠AOD=α+β,
∵OE平分∠AOD,
∴∠DOE= ![]() (α+β),
(α+β),
∴∠COE=∠DOE﹣∠COD= ![]() ,
,
如图3,∵∠AOC=∠BOD=α,∠COD=β,
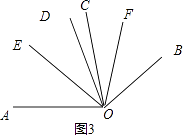
∴∠AOD=α+β,
∵OE平分∠AOD,
∴∠DOE= ![]() (α﹣β),
(α﹣β),
∴∠COE=∠DOE+∠COD= ![]() .
.
综上所述: ![]() ,
,
所以答案是: ![]() .
.
【考点精析】利用角的平分线和角的运算对题目进行判断即可得到答案,需要熟知从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;角之间可以进行加减运算;一个角可以用其他角的和或差来表示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A、B、C、D在⊙O上,AB∥CD,AB=24,CD=10,⊙O的半径为13,求梯形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价.水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断( )
①年用水量不超过180m3的该市居民家庭按第一档水价交费;
②年用水量超过240m3的该市居民家庭按第三档水价交费;
③该市居民家庭年用水量的中位数在150﹣180之间;
④该市居民家庭年用水量的平均数不超过180.
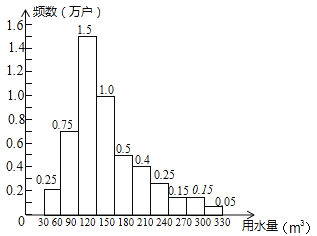
A.①③ B.①④ C.②③ D.②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红在月历的同一列上圈出相邻的三个数,若算出它们的和是39,则该列第一个数是( )
A.6
B.12
C.13
D.14 -
科目: 来源: 题型:
查看答案和解析>>【题目】在国务院办公厅发布《中国足球发展改革总体方案》之后,某校为了调查本校学生对足球知识的了解程度,随机抽取了部分学生进行一次问卷调查,并根据调查结果绘制了如图的统计图,请根据图中所给的信息,解答下列问题:
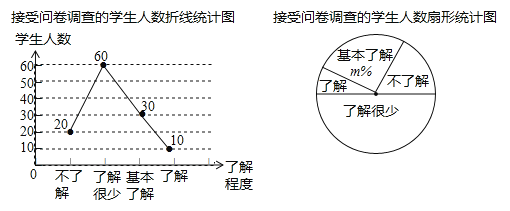
(1)本次接受问卷调查的学生总人数是 ;
(2)扇形统计图中,“了解”所对应扇形的圆心角的度数为 ,m的值为 ;
(3)若该校共有学生1500名,请根据上述调查结果估算该校学生对足球的了解程度为“基本了解”的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】作图题:(不要求写作法)如图,△ABC在平面直角坐标系中,其中,点A,B,C的坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).

(1)作△ABC关于y轴对称的△A1B1C1 , 其中,点A、B、C的对应点分别为A1、B1、C1;
(2)写出点A1、B1、C1的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
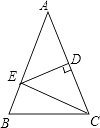
(1)求∠BEC的度数.
(2)若CE=5,求BC的长.
相关试题

