搜索
【题目】已知点A、B、C、D在⊙O上，AB∥CD，AB=24，CD=10，⊙O的半径为13，求梯形ABCD的面积．
参考答案：
【答案】解：如图1所示：过点O作OE⊥CD，OF⊥AB， 且EF必过点O，
∵AB∥CD，AB=24cm，CD=10cm，圆O的直径为26cm，
∴EC=5cm，BF=12cm，
∴EO=12cm，FO=5cm，
则EF=17cm，
故梯形ABCD的面积为： 
（10+24）×17=289（cm2），
如图2，同理可得出：EF=12﹣5=7（cm），
则梯形ABCD的面积为： （10+24）×7=119（cm2）．
综上所述：梯形ABCD的面积为289cm2或119cm2 ．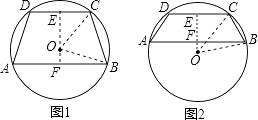 
【解析】根据题意画出图形，进而分类讨论得出EF的长，进而求出面积即可．
【考点精析】掌握梯形的定义是解答本题的根本，需要知道一组对边平行，另一组对边不平行的四边形是梯形．两腰相等的梯形是等腰梯形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法中，错误的是（ ）
A．平行四边形的对角线互相平分
B．对角线互相平分的四边形是平行四边形
C．菱形的对角线互相垂直
D．对角线互相垂直的四边形是菱形
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列各式中，正确的是（ ）
A.|﹣0.1|＜0
B.
＜﹣|﹣ 
?|
C.
＞0.86
D.﹣2=﹣|﹣2| -
科目： 来源： 题型：
查看答案和解析>>【题目】已知如图，AB是半圆O的直径，弦AD、BC相交于点P，那么
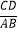等于∠BPD的（ ） 
A.正弦
B.余弦
C.正切
D.以上都不对 -
科目： 来源： 题型：
查看答案和解析>>【题目】为了节约水资源，某市准备按照居民家庭年用水量实行阶梯水价．水价分档递增，计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%，15%和5%，为合理确定各档之间的界限，随机抽查了该市5万户居民家庭上一年的年用水量（单位：m3），绘制了统计图．如图所示，下面四个推断（ ）
①年用水量不超过180m3的该市居民家庭按第一档水价交费；
②年用水量超过240m3的该市居民家庭按第三档水价交费；
③该市居民家庭年用水量的中位数在150﹣180之间；
④该市居民家庭年用水量的平均数不超过180．
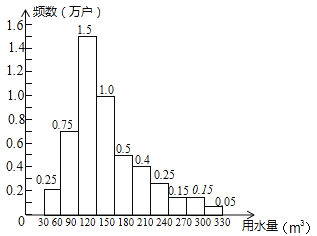
A．①③ B．①④ C．②③ D．②④
-
科目： 来源： 题型：
查看答案和解析>>【题目】小红在月历的同一列上圈出相邻的三个数，若算出它们的和是39，则该列第一个数是（ ）
A.6
B.12
C.13
D.14 -
科目： 来源： 题型：
查看答案和解析>>【题目】综合题
（1）如图1，若CO⊥AB，垂足为O，OE、OF分别平分∠AOC与∠BOC．求∠EOF的度数；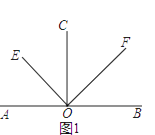
（2）如图2，若∠AOC=∠BOD=80°，OE、OF分别平分∠AOD与∠BOC．求∠EOF的度数；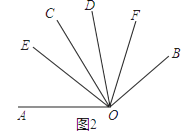
（3）若∠AOC=∠BOD=α，将∠BOD绕点O旋转，使得射线OC与射线OD的夹角为β，OE、OF分别平分∠AOD与∠BOC．若α+β≤180°，α＞β，则∠EOC= ． （用含α与β的代数式表示）
相关试题
