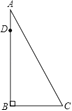
【题目】如图,AB为一棵大树,在树上距地面10米的D处有两只猴子,他们同时发现C处有一筐水果,一只猴子从D处往上爬到树顶A处,又沿滑绳AC滑到C处,另一只猴子从D滑到B,再由B跑到C处,已知两只猴子所经路程都为15米,求树高AB.
参考答案:
【答案】12米
【解析】分析:在Rt△ABC中,∠B=90°,则满足AB+BC=AC,BC=a(米),AC=b(米),AD=x(米),根据两只猴子经过的路程一样可得10+a=x+b=15解方程组可以求x的值,即可计算树高=10+x.
Rt△ABC中,∠B=90°,
本题解析:
设BC=a(米),AC=b(米),AD=x(米)
则10+a=x+b=15(米).
∴a=5(米),b=15x(米)
又在Rt△ABC中,由勾股定理得:(10+x)+a=b,
∴(10+x)+5=(15x),
解得,x=2,即AD=2(米)
∴AB=AD+DB=2+10=12(米)
答:树高AB为12米。
-
科目: 来源: 题型:
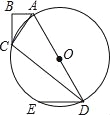
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=6,BC=8,CD=24,AD=26,∠B=90°,以AD为直径作圆O,过点D作DE∥AB交圆O于点E
(1)证明点C在圆O上;
(2)求tan∠CDE的值;
(3)求圆心O到弦ED的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(x﹣2)2+3的顶点坐标是( )
A.(2,3)B.(﹣2,3)C.(2,﹣3)D.(﹣2,﹣3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆柱底面周长为4cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为________cm.

-
科目: 来源: 题型:
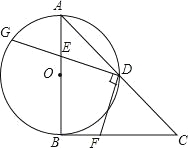
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF;
(2)连接GB,EF,求证:GB∥EF;
(3)若AE=1,EB=2,求DG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=﹣x+2沿y轴向上平移2个单位后与x轴的交点坐标是( )
A.(4,0)
B.(0,4)
C.(2,0)
D.(0,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,在Rt△ABC和Rt△DBE中,∠ABC=∠DBE=90°,AB=BC=3,BD=BE=1,连结CD,AE.
求证:△BCD≌△BAE.
(2)在(1)的条件下,当
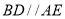 时,延长CD交AE于点F,如图②,求AF的长.
时,延长CD交AE于点F,如图②,求AF的长.(3)在(2)的条件下,线段BC上是否存在一点P,使得△PBD为等腰三角形?若存在,请直接写出满足△PBD为等腰三角形时,线段PB的长;若不存在,请说明理由.

相关试题

