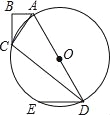
【题目】如图,在四边形ABCD中,AB=6,BC=8,CD=24,AD=26,∠B=90°,以AD为直径作圆O,过点D作DE∥AB交圆O于点E
(1)证明点C在圆O上;
(2)求tan∠CDE的值;
(3)求圆心O到弦ED的距离.
参考答案:
【答案】(1)详见解析;(2)![]() ;(3)圆心O到弦ED的距离为
;(3)圆心O到弦ED的距离为![]() .
.
【解析】
试题分析:(1)如图1,连结CO.先由勾股定理求出AC=10,再利用勾股定理的逆定理证明△ACD是直角三角形,∠C=90°,那么OC为Rt△ACD斜边上的中线,根据直角三角形斜边上的中线等于斜边的一半得出OC=![]() AD=r,即点C在圆O上;(2)如图2,延长BC、DE交于点F,∠BFD=90°.根据同角的余角相等得出∠CDE=∠ACB.在Rt△ABC中,利用正切函数定义求出tan∠ACB=
AD=r,即点C在圆O上;(2)如图2,延长BC、DE交于点F,∠BFD=90°.根据同角的余角相等得出∠CDE=∠ACB.在Rt△ABC中,利用正切函数定义求出tan∠ACB=![]() =
=![]() ,则tan∠CDE=tan∠ACB=
,则tan∠CDE=tan∠ACB=![]() ;(3)如图3,连结AE,作OG⊥ED于点G,则OG∥AE,且OG=
;(3)如图3,连结AE,作OG⊥ED于点G,则OG∥AE,且OG=![]() AE.易证△ABC∽△CFD,根据相似三角形对应边成比例求出CF=
AE.易证△ABC∽△CFD,根据相似三角形对应边成比例求出CF=![]() ,那么BF=BC+CF=
,那么BF=BC+CF=![]() .再证明四边形ABFE是矩形,得出AE=BF=
.再证明四边形ABFE是矩形,得出AE=BF=![]() ,所以OG=
,所以OG=![]() AE=
AE=![]() .
.
试题解析:(1)证明:如图1,连结CO.
∵AB=6,BC=8,∠B=90°,
∴AC=10.
又∵CD=24,AD=26,102+242=262,
∴△ACD是直角三角形,∠C=90°.
∵AD为⊙O的直径,
∴AO=OD,OC为Rt△ACD斜边上的中线,
∴OC=![]() AD=r,
AD=r,
∴点C在圆O上;
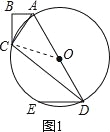
(2)解:如图2,延长BC、DE交于点F,∠BFD=90°.
∵∠BFD=90°,
∴∠CDE+∠FCD=90°,
又∵∠ACD=90°,
∴∠ACB+∠FCD=90°,
∴∠CDE=∠ACB.
在Rt△ABC中,tan∠ACB=![]() =
=![]() ,
,
∴tan∠CDE=tan∠ACB=![]() ;
;
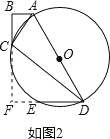
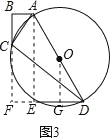
(3)解:如图3,连结AE,作OG⊥ED于点G,则OG∥AE,且OG=![]() AE.
AE.
易证△ABC∽△CFD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴CF=![]() ,
,
∴BF=BC+CF=8+![]() =
=![]() .
.
∵∠B=∠F=∠AED=90°,
∴四边形ABFE是矩形,
∴AE=BF=![]() ,
,
∴OG=![]() AE=
AE=![]() ,
,
即圆心O到弦ED的距离为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列所述图形中,是轴对称图形又是中心对称图形的是 ( )
A.平行四边形B.等边三角形C.正五边形D.菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a2a3=a6
B.(﹣m2)3=﹣m6
C.b6÷b3=b2
D.3a+3b=6ab -
科目: 来源: 题型:
查看答案和解析>>【题目】当m=-1时,下列代数式是五次三项式的是( ).
A. y4-m-1 B. 54-m+2xm-4+5y C. 2am+6-5ab+bm D. a|m|+4-b3+c
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(x﹣2)2+3的顶点坐标是( )
A.(2,3)B.(﹣2,3)C.(2,﹣3)D.(﹣2,﹣3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆柱底面周长为4cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为________cm.

-
科目: 来源: 题型:
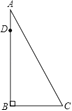
查看答案和解析>>【题目】如图,AB为一棵大树,在树上距地面10米的D处有两只猴子,他们同时发现C处有一筐水果,一只猴子从D处往上爬到树顶A处,又沿滑绳AC滑到C处,另一只猴子从D滑到B,再由B跑到C处,已知两只猴子所经路程都为15米,求树高AB.
相关试题

