Question

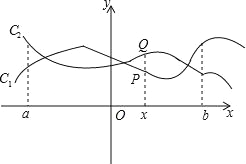
【题目】如图，点P（x，y1）与Q（x，y2）分别是两个函数图象C1与C2上的任一点．当a≤x≤b时，有﹣1≤y1﹣y2≤1成立，则称这两个函数在a≤x≤b上是“相邻函数”，否则称它们在a≤x≤b上是“非相邻函数”．例如，点P（x，y1）与Q（x，y2）分别是两个函数y=3x+1与y=2x﹣1图象上的任一点，当﹣3≤x≤﹣1时，y1﹣y2=（3x+1）﹣（2x﹣1）=x+2，通过构造函数y=x+2并研究它在﹣3≤x≤﹣1上的性质，得到该函数值的范围是﹣1≤y≤1，所以﹣1≤y1﹣y2≤1成立，因此这两个函数在﹣3≤x≤﹣1上是“相邻函数”．

（1）判断函数y=3x+1与y=2x+2在0≤x≤2上是否为“相邻函数”，并说明理由；

（2）若函数y=x2﹣x与y=xa在0≤x≤2上是“相邻函数”，求a的取值范围．

Answer 1

【答案】（1）函数y=3x+1与y=2x+2在0≤x≤2上是“相邻函数”，理由见解析；

（2）若函数y=x2﹣x与y=xa在0≤x≤2上是“相邻函数”，则a的取值范围为≤a≤1．

【解析】分析：（1）通过构建函数y=x-1，根据一次函数的性质可得出该函数在0≤x≤2上单调递增，分别代入x=0、x=2即可得出y的取值范围，由此即可得出结论；（2）由函数y=-x与y=xa在0≤x≤2上是“相邻函数”，构造函数y=-（a+1）x，根据抛物线的位置不同，令其最大值≤1、最小值≥-1，解关于a的不等式组即可得出结论．

本题解析：（1）函数y=3x+1与y=2x+2在0 ≤ x≤ 2上是“相邻函数”，理由如下：

点P（x，y1）与Q　（x，y2）分别是两个函数y=3x+1与y=2x+2图象上的任一点，

当0≤ x≤ 2时，y1﹣y2=（3x+1）﹣（2x+2）=x﹣1，通过构造函数y=x﹣1并研究它在0≤ x≤ 2上的性质，得到该函数值的范围是﹣1 ≤ y ≤1，所以﹣1 ≤ y1﹣y2 ≤1成立，

因此这两个函数在0 ≤ x ≤2上是“相邻函数”．

（2）∵函数y=x2﹣x与y= x a在0 ≤ x ≤2上是“相邻函数”，

∴构造函数y=x2﹣（a+1）x，在0 ≤ x ≤2上﹣1 ≤ y ≤1．

根据抛物线y=x2﹣（a+1）x对称轴的位置不同，来考虑：

①当≤0，即a≤﹣1时（图1），

，解得：a≥ ，

∴此时无解；

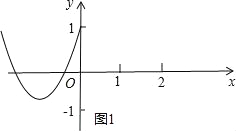
②当0＜ ≤1，即﹣1＜a≤1时（图2），

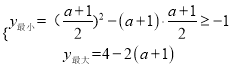，解得： ≤a≤1，

∴≤a≤1；

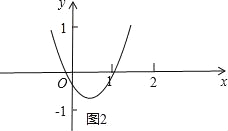
③当1＜≤2，即1＜a≤3时（图3），

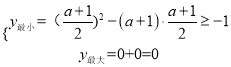，解得：﹣3≤a≤1，

∴此时无解；

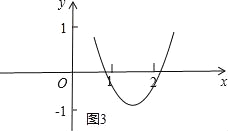
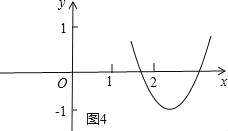
④当2＜，即a＞3时（图4），

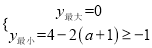，解得：a≤ ，

∴此时无解．

综上可知：若函数y=x2﹣x与y=xa在0≤x≤2上是“相邻函数”，则a的取值范围为≤a≤1．