【题目】如图,上、下底面为全等的正六边形礼盒,其主视图与左视图均由矩形构成,主视图中大矩形边长如图所示,左视图中包含两个全等的矩形,如果用彩色胶带按如图所示的方式包扎礼盒,那么所需胶带长度至少为多少厘米?(结果精确到1 cm)

参考答案:
【答案】432cm
【解析】分析:由主视图知道,高是20 cm,两顶点之间的最大距离为60 cm,应利用正六边形的性质求得底面对边之间的距离,然后所有棱长相加即可.
本题解析:
根据题意,作出实际图形的上底面,如解图.AC,CD是上底面的两边,过点C作CB⊥AD于点B.易得∠ACD=120°,AC=CD,CB⊥AD,∴∠CDB=30°,∴CB=![]() CD.
CD.
∵最长对角线长60 cm,∴2CB+CD=60 cm,∴CB=15 cm,CD=30 cm,∴BD=15![]() ,∴AD=30
,∴AD=30![]() cm.∴胶带的长至少为30
cm.∴胶带的长至少为30![]() ×6+20×6≈432(cm)
×6+20×6≈432(cm)

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:
 .
.(2)解不等式
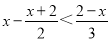 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
(3)解方程组:
 .
. -
科目: 来源: 题型:
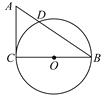
查看答案和解析>>【题目】如图,在Rt△ACB中,∠C=90°,AC=3 cm,BC=4 cm,以BC为直径作⊙O交AB于点D.
(1)求线段AD的长度;
(2)点E是线段AC上的一点,试问当点E在什么位置时,直线ED与⊙O相切?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ACB中,∠ACB=90°,AC=3,BC=4,有一过点C的动圆⊙O与斜边AB相切于动点P,连接CP.
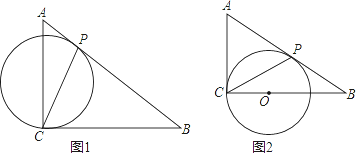
(1)当⊙O与直角边AC相切时,如图2所示,求此时⊙O的半径r的长;
(2)随着切点P的位置不同,弦CP的长也会发生变化,试求出弦CP的长的取值范围.
(3)当切点P在何处时,⊙O的半径r有最大值?试求出这个最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具厂加工了一批玩具“六一”捐赠给儿童福利院,甲、乙两车间同时开始加工这批玩具,加工一段时间后,甲车间的设备出现故障停产一段时间,乙车间继续加工,甲维修好设备后继续按照原来的工作效率加工,从工作开始到加工完这批玩具乙车间工作
 小时,甲、乙两车间加工玩具的总数量
小时,甲、乙两车间加工玩具的总数量 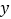 (件)与加工时间
(件)与加工时间  (时)之间的函数图象如图所示.
(时)之间的函数图象如图所示.(1)求乙车间每小时加工玩具的数量.
(2)求甲车间维修完设备后,
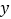 与
与  之间的函数关系式.
之间的函数关系式.(3)何时能加工一半?
-
科目: 来源: 题型:
查看答案和解析>>【题目】当
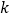 值相同时,我们把正比例函数
值相同时,我们把正比例函数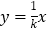 与反比例函数
与反比例函数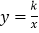 叫做“关联函数”,可以通过图象研究“关联函数”的性质.小明根据学习函数的经验,先以
叫做“关联函数”,可以通过图象研究“关联函数”的性质.小明根据学习函数的经验,先以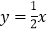 与
与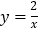 为例对“关联函数”进行了探究.下面是小明的探究过程,请你将它补充完整.
为例对“关联函数”进行了探究.下面是小明的探究过程,请你将它补充完整.(1)如图,在同一坐标系中画出这两个函数的图象.设这两个函数图象的交点分别为
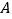 ,
,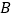 ,则点
,则点 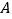 的坐标为
的坐标为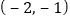 ,点
,点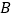 的坐标为_______;
的坐标为_______;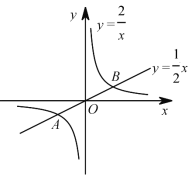
(2)点
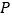 是函数
是函数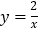 在第一象限内的图象上一个动点(点
在第一象限内的图象上一个动点(点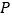 不与点
不与点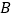 重合),设点
重合),设点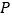 的坐标为
的坐标为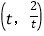 ,其中
,其中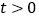 且
且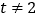 .
.①结论
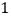 :作直线
:作直线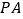 ,
,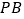 分别与
分别与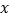 轴交于点
轴交于点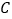 ,
,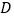 ,则在点
,则在点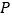 运动的过程中,总有
运动的过程中,总有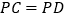 .
.证明:设直线
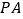 的解析式为
的解析式为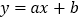 ,将点
,将点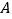 和点
和点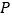 的坐标代入,得
的坐标代入,得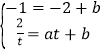
解得
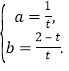 则直线
则直线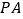 的解析式为
的解析式为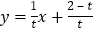 .
.令
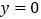 ,可得
,可得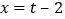 ,则点
,则点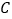 的坐标为
的坐标为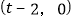 .
.同理可求,直线
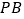 的解析式为
的解析式为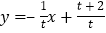 ,点
,点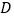 的坐标为________.
的坐标为________.请你继续完成证明
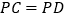 的后续过程:
的后续过程:②结论
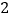 :设
:设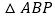 的面积为
的面积为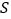 ,则
,则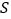 是
是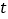 的函数.请你直接写出
的函数.请你直接写出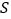 与
与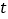 的函数表达式.
的函数表达式. -
科目: 来源: 题型:
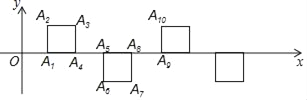
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,OA1=1,将边长为1的正方形一边与x轴重合按图中规律摆放,其中每两个正方形的间距都是1,则点A2017的坐标为 .
相关试题

