【题目】王卉同学从家出发沿笔直的公路去晨练,他离开家的距离y(米)与时间x(分钟)的函数关系图象如图所示,下列结论正确的个数是( )
①整个行进过程花了30分钟;
②整个行进过程共走了1 000米;
③前10分钟的速度越来越快;
④在途中停下来休息了5分钟;
⑤返回时速度为100米/分钟.

A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】C
【解析】
①由当y=0时,x=0或x=30即可得出①正确;②观察函数图象找出y的最大值,乘2即可得出②错误;③由前10分钟的函数图象为线段可知为匀速运动,即③错误;④由AB段平行于x轴,用15﹣10即可得出④正确;⑤根据速度=路程÷时间即可算出返回时速度为100米/分,即⑤正确.
综上即可得出结论.
①∵当y=0时,x=0或x=30,∴整个行进过程花了30分钟,①正确;
②观察函数图象可知,y的最大值为1000.
∵1000×2=2000(米),∴整个行进过程共走了2000米,②错误;
③∵当0≤x≤10时,函数图象为线段,∴前10分钟为匀速运动,③错误;
④∵15﹣10=5(分钟),∴在途中停下来休息了5分钟,④正确;
⑤∵1000÷(30﹣20)=100(米/分),∴返回时速度为100米/分,⑤正确.
综上所述:正确的结论有①④⑤.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
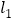 ∥
∥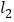 ,且
,且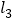 和
和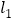 ,
,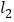 分别交于A,B两点,
分别交于A,B两点,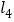 和
和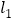 ,
,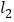 相交于C,D两点,点P在直线AB上,
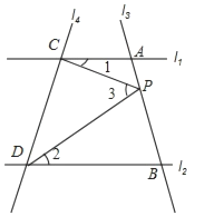
相交于C,D两点,点P在直线AB上,(1)当点P在A,B两点间运动时,问∠1,∠2,∠3之间的关系是否发生变化?如果不发生变化它们之间满足什么关系?并说明理由;
(2)如果点P在A,B两点外侧运动时,试探究∠ACP,∠BDP,∠CPD之间的关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,给出下列判断:①若△AEF是等边三角形,则∠B=60°,②若∠B=60°,则△AEF是等边三角形,③若AE=AF,则平行四边形ABCD是菱形,④若平行四边形ABCD是菱形,则AE=AF,其中,结论正确的是__________(只需填写正确结论的序号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算:( ﹣2)0﹣(﹣1)2017+
﹣2)0﹣(﹣1)2017+  ﹣sin45°;
﹣sin45°;
(2)化简:( ﹣
﹣  )÷
)÷  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列推理及所注明的理由都正确的是:( )
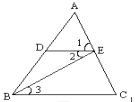
A. 因为DE∥BC,所以∠1=∠C(同位角相等,两直线平行)
B. 因为∠2=∠3,所以DE∥BC(两直线平行,内错角相等)
C. 因为DE∥BC,所以∠2=∠3(两直线平行,内错角相等)
D. 因为∠1=∠C,所以DE∥BC(两直线平行,同位角相等)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.
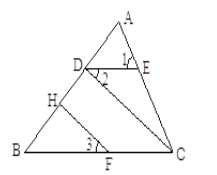
证明:∵∠1=∠ACB(已知)
∴DE∥BC( )
∴∠2= ( )
∵∠2=∠3(已知)
∴∠3=
∴CD∥FH( )
∴∠BDC=∠BHF( )
又∵FH⊥AB(已知)
∴ ( )
∵CD∥FH
∴∠BHF=∠BDC=90°( )
即CD⊥AB( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,BD是矩形ABCD的对角线,∠ABD=30°,AD=1.将△BCD沿射线BD方向平移到△B'C'D'的位置,使B'为BD中点,连接AB',C'D,AD',BC',如图②.
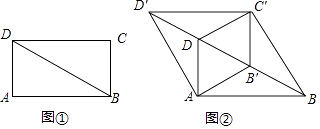
(1)求证:四边形AB'C'D是菱形;
(2)四边形ABC'D′的周长为;
(3)将四边形ABC'D'沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
相关试题

