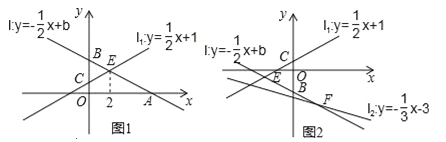
【题目】如图，已知直线l：y=﹣x+b与x轴、y轴分别交于点A，B，直线l1：y=x+1与y轴交于点C，设直线l与直线l1的交点为E

（1）如图1，若点E的横坐标为2，求点A的坐标；

（2）在（1）的前提下，D（a，0）为x轴上的一点，过点D作x轴的垂线，分别交直线l与直线l1于点M、N，若以点B、C、M、N为顶点的四边形为平行四边形，求a的值；

（3）如图2，设直线l与直线l2：y=﹣x﹣3的交点为F，问是否存在点B，使BE=BF，若存在，求出直线l的解析式，若不存在，请说明理由．

参考答案：

【答案】（1）点A的坐标为（6，0）；

（2）当以点B、C、M、N为顶点的四边形为平行四边形，a的值为4；

（3）存在点B，使BE=BF，此时直线l的解析式为y=﹣x﹣．

【解析】试题分析：（1）由点E的横坐标结合一次函数图象上点的坐标特征即可找出点E的坐标，再利用待定系数法即可求出直线的解析式，令求出的值，即可得出点A的坐标；

（2）根据点D的横坐标为a利用一次函数图象上点的坐标特征即可找出点M、N的坐标，从而得出线段MN的长度，分别令直线的解析式中求出点的坐标，再根据平行四边形的性质即可得出关于a的含绝对值符号的一元一次方程，解方程即可得出结论；

（3）假设存在，联立直线的解析式成方程组，解方程组求出点E的坐标，联立直线的解析式成方程组，解方程组求出点F的坐标，结合即可得出关于b的一元一次方程，解方程求出b值，此题得解．

试题解析：(1)∵点E在直线l1上，且点E的横坐标为2，

∴点E的坐标为(2,2)，

∵点E在直线l上，

解得：b=3，

∴直线l的解析式为

当y=0时,有

解得：x=6,

∴点A的坐标为(6,0).

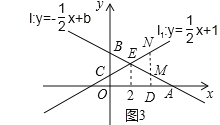
(2)依照题意画出图形，如图3所示,

当x=a时，

当x=0时,

∴BC=31=2.

∵BC∥MN，

∴当MN=BC=2时，以点B. C.M、N为顶点的四边形为平行四边形，

此时|a2|=2，

解得：a=4或a=0(舍去).

∴当以点B. C.M、N为顶点的四边形为平行四边形，a的值为4.

(3)假设存在.

联立直线l、l1的解析式成方程组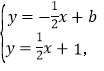

解得：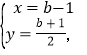

∴点E的坐标为

联立直线l、l2的解析式成方程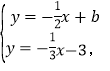

解得：

∴点F的坐标为(18+6b,92b).

∵BE=BF，且E.F均在直线l上，

∴b1=186b,解得：

此时直线l的解析式为

故存在点B,使BE=BF,此时直线l的解析式为

关闭