【题目】如图,在直角坐标系中,半径为1的⊙A圆心与原点O重合,直线l分别交x轴、y轴于点B、C,若点B的坐标为(6,0),tan∠ABC=![]() .
.

(1)若点P是⊙A 上的动点,求P到直线BC的最小距离,并求此时点P的坐标;
(2)若点A从原点O出发,以1个单位/秒的速度沿着线路OB→BC→CO运动,回到点O停止运动,⊙A随着点A的运动而移动.设点A运动的时间为t.
①求⊙A在整个运动过程中与坐标轴相切时t的取值;
②求⊙A在整个运动过程中所扫过的图形的面积为 .
参考答案:
【答案】(1)![]() ,最小距离为3.8;(2)①
,最小距离为3.8;(2)①![]() 1、
1、![]() 、
、![]() 、
、![]() 、
、![]() 、23;②42+
、23;②42+![]()
【解析】
试题分析:(1)利用点B的坐标为(6,0)且tan∠ABC=![]() ,即可得出C点坐标,进而利用△OPH∽△CBO,求出P点坐标即可;
,即可得出C点坐标,进而利用△OPH∽△CBO,求出P点坐标即可;
(2)①利用⊙A在整个运动过程中所扫过的面积=矩形DROC面积+矩形OYHB面积+矩形BGFC面积+△ABC面积+一个圆的面积-△LSK面积,求出即可;
②利用相似三角形的判定与性质得出t的值即可,注意利用数形结合得出.
(1)∵点B的坐标为(6,0)且tan∠ABC=![]()
![]()
![]()
∴AC=8,
故C点坐标为:C(0,8),
∴BC=10,
过O作OG⊥BC于G,则OG与⊙A的交点即为所求点P.过P作PH⊥x轴于H,

∵PH⊥AB,
∴∠OHP=90°,
∵∠POH+∠COP=90°,∠POC+∠OCG=90°,
∴∠POH=∠OCG,
又∵∠COB=90°,
∴△OPH∽△CBO,
![]()
可得![]() ,
,![]()
∴![]() ;
;
(2)①如图所示:⊙A与△OBC的三边相切有6种不同的情况,
当⊙O2与BC相切于点N,则O2N⊥BC,

∵∠OBC=∠O2BN,∠O2NB=∠COB=90°,
∴△O2NB∽△COB,

解得![]()
则![]() ,则t的值为
,则t的值为![]() 秒,
秒,
同理可得出:O,O4,O5的位置,即可得出时间t的值,
故t=1、![]() 、
、![]() 、
、![]() 、
、![]() 、23;
、23;
②如图2所示:当圆分别在O,B,C位置时,作出公切线DR,YH,FG,PW,切点分别为:D,R,H,G,F,P,W
连接CD,CF,BG,过点K作KX⊥BC于点X,PW交AB于点U,

∵PU∥OB,
∴∠OBC=∠KUX,
∵∠KXU=∠COB=90°,
∴△COB∽△KXU,

∵PU∥BO,
∴△CPU∽△COB,

同理可得出:△LSK∽△COB,

解得:LS=4,
则∠CDR=∠CFG=∠BGF=∠BHY=∠AYH=90°,
故⊙A在整个运动过程中所扫过的面积
=矩形DROC面积+矩形OYHB面积+矩形BGFC面积+△ABC面积+一个圆的面积-△LSK面积,
![]()
=42+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l:y=﹣
 x+b与x轴、y轴分别交于点A,B,直线l1:y=
x+b与x轴、y轴分别交于点A,B,直线l1:y= x+1与y轴交于点C,设直线l与直线l1的交点为E
x+1与y轴交于点C,设直线l与直线l1的交点为E(1)如图1,若点E的横坐标为2,求点A的坐标;
(2)在(1)的前提下,D(a,0)为x轴上的一点,过点D作x轴的垂线,分别交直线l与直线l1于点M、N,若以点B、C、M、N为顶点的四边形为平行四边形,求a的值;
(3)如图2,设直线l与直线l2:y=﹣
 x﹣3的交点为F,问是否存在点B,使BE=BF,若存在,求出直线l的解析式,若不存在,请说明理由.
x﹣3的交点为F,问是否存在点B,使BE=BF,若存在,求出直线l的解析式,若不存在,请说明理由.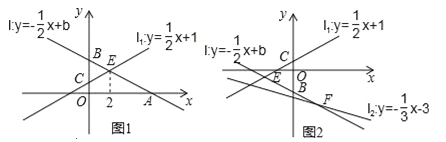
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,以点(3,-5)为圆心,r为半径的圆上有且仅有两点到x轴所在直线的距离等于1,则圆的半径r的取值范围是 ( )
A.r>4 B.0<r<6 C.4≤r<6 D.4<r<6
-
科目: 来源: 题型:
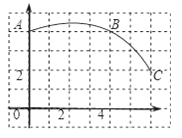
查看答案和解析>>【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
-
科目: 来源: 题型:
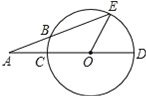
查看答案和解析>>【题目】已知,如图,CD为⊙O的直径,∠EOD=60°,AE交⊙O于点B,E,且AB=OC,求:(1)∠A的度数;(2)∠AEO度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:8(x+3)=3(x﹣2)
相关试题

