【题目】已知二次函数y=x2﹣x﹣6.
(1)画出函数的图象;
(2)观察图象,指出方程x2﹣x﹣6=0的解及不等式x2﹣x﹣6>0解集;
(3)求二次函数的图象与坐标轴的交点所构成的三角形的面积.
参考答案:
【答案】(1)图形见解析
(2)x<﹣2或x>3;
(3)三角形的面积为15.
【解析】试题分析:(1)由抛物线开口方向,与x轴交点坐标,顶点坐标画出图象;
(2)根据图象直接写出答案;
(3)由三角形的面积公式进行解答.
试题解析:(1)函数图象如下:
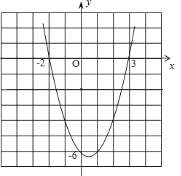
(2)由抛物线解析式y=x2﹣x﹣6知,抛物线与x轴的交点坐标是(3,0),(﹣2,0),
方程x2﹣x﹣6=0的解是x1=﹣2,x2=3;
不等式x2﹣x﹣6>0的解集为x<﹣2或x>3;
(3)如图所示:抛物线与坐标轴所构成的三角形面积是:![]() ×|﹣2﹣3|×|﹣6|=15.
×|﹣2﹣3|×|﹣6|=15.
即抛物线与坐标轴所构成的三角形面积是15三角形的面积为15.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:﹣5x+9=7x﹣15.
-
科目: 来源: 题型:
查看答案和解析>>【题目】0.252018×(﹣4)2019=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明设计了点做圆周运动的一个动画游戏,如上图所示,甲、乙两点分别从直径的两端点A、B以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程l(cm)与时间t(s)满足关系:l=
 t2+
t2+ t(t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.
t(t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.(1)甲运动4s后的路程是多少?
(2)甲、乙从开始运动到第一次相遇时,它们运动了多少时间?
(3)甲、乙从开始运动到第二次相遇时,它们运动了多少时间?

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两工程队维修同一段路面,甲队先清理路面,乙队在甲队清理后铺设路面.乙队在中途停工了一段时间,然后按停工前的工作效率继续工作.在整个工作过程中,甲队清理完的路面长y(米)与时间x(时)的函数图象为线段OA,乙队铺设完的路面长y(米)与时间x(时)的函数图象为折线BC-CD-DE,如图所示,从甲队开始工作时计时.
(1)分别求线段BC、DE所在直线对应的函数关系式.
(2)当甲队清理完路面时,求乙队铺设完的路面长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l:y=﹣
 x+b与x轴、y轴分别交于点A,B,直线l1:y=
x+b与x轴、y轴分别交于点A,B,直线l1:y= x+1与y轴交于点C,设直线l与直线l1的交点为E
x+1与y轴交于点C,设直线l与直线l1的交点为E(1)如图1,若点E的横坐标为2,求点A的坐标;
(2)在(1)的前提下,D(a,0)为x轴上的一点,过点D作x轴的垂线,分别交直线l与直线l1于点M、N,若以点B、C、M、N为顶点的四边形为平行四边形,求a的值;
(3)如图2,设直线l与直线l2:y=﹣
 x﹣3的交点为F,问是否存在点B,使BE=BF,若存在,求出直线l的解析式,若不存在,请说明理由.
x﹣3的交点为F,问是否存在点B,使BE=BF,若存在,求出直线l的解析式,若不存在,请说明理由.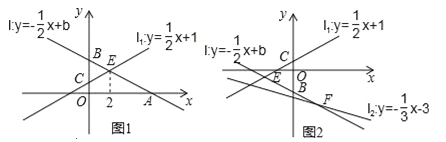
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.

相关试题

