搜索
【题目】如图，一次函数y=kx+b与反比例函数y= 
的图象交于A（2，3），B（﹣3，n）两点． 
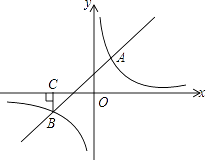
（1）求反比例函数的解析式；
（2）过B点作BC⊥x轴，垂足为C，若P是反比例函数图象上的一点，连接PC，PB，求当△PCB的面积等于5时点P的坐标．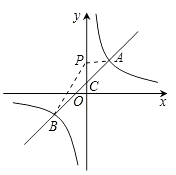 
参考答案：
【答案】
（1）解：∵反比例函数y= 
的图象经过点A（2，3），
∴m=6．
∴反比例函数的解析式是y= 
（2）解：∵B点（﹣3，n）在反比例函数y= 的图象上，
∴n=﹣2，
∴B（﹣3，﹣2），
∴BC=2，设△PBC在BC边上的高为h，
则 
BCh=5，
∴h=5，
∵P是反比例函数图象上的一点，
∴点P的横坐标为：﹣8或2，
∴点P的坐标为（﹣8，﹣ 
），（2，3）．
【解析】（1）将A坐标代入反比例函数解析式中求出m的值，即可确定出反比例函数解析式；（2）由B点（﹣3，n）在反比例函数y= 的图象上，于是得到B（﹣3，﹣2），求得BC=2，设△PBC在BC边上的高为h，根据三角形的面积公式列方程即可得到结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】将分别标有数字1，2，3的三张卡片洗匀后，背面朝上放在桌面上．
（1）随机地抽取一张，求P（奇数）；
（2）随机地抽取一张作为十位上的数字（不放回），再抽取一张作为个位上的数字，求组成的两位数是4的倍数的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】（1）把数轴补充完整；
（2）在数轴上表示下列各数: 3,
, 
, 
；（3）用“<”连接起来.________________________________;
（4）
与之间的距离是_______________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AB与CD相交于点O，OD恰为∠BOE的平分线．
(1)图中∠BOC的补角是 把符合条件的角都填出来)；
(2)若∠AOD＝145°，求∠AOE的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】探索题
图a是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图b的形状拼成一个正方形．
（1）你认为图b中的影部分的正方形的边长等于 ．
（2）请用两种不同的方法求图b中阴影部分的面积．
方法1： (只列式，不化简）
方法2： (只列式，不化简）
（3）观察图b你能写出下列三个代数式之间的等量关系吗？
代数式：(m+n)2，(m-n)2，
．（4）根据（3）题中的等量关系，解决如下问题：若a+b=8，ab=5，则 (a-b)2= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在对某地区的一次人口抽样统计分析中，各年龄段(年龄为整数)的人数如下表所示．请根据此表回答下列问题：
年龄段
0～9
10～19
20～29
30～39
40～49
50～59
60～69
70～79
80～89
人数
9
11
17
18
17
12
8
6
2
(1)这次共调查了多少人？
(2)哪个年龄段的人数最多？哪个年龄段的人数最少？
(3)年龄在60岁以上(含60岁)的频数是多少？所占百分比是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，点P是弦AC上一动点（不与A，C重合），过点P作PD⊥AB，垂足为D，射线DP交
于点E，交过点C的切线于点F． 
（1）求证：FC=FP；
（2）若∠CAB=30°，当E是 的中点时，判断以A，O，C，E为顶点的四边形是什么特殊四边形，并说明理由．
相关试题
