【题目】如图,菱形ABCD的边长是4cm,E是AB的中点,且DE⊥AB,则菱形ABCD的面积为cm2 . 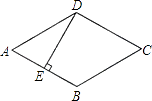
参考答案:
【答案】8 ![]()
【解析】解:∵四边形ABCD是菱形, ∴AD=AB=4,
∵AE=EB=2,
∵DE⊥AB,
∴∠AED=90°
在Rt△ADE中,DE= ![]() =2
=2 ![]() ,
,
∴菱形ABCD的面积=ABDE=42 ![]() =8
=8 ![]() ,
,
所以答案是8 ![]() .
.
【考点精析】通过灵活运用线段垂直平分线的性质和菱形的性质,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正数m的两个不同平方根分别是2a-1与-a+2,则这个正数m=______
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为5,则正方形A,B,C,D的面积的和为
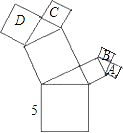
-
科目: 来源: 题型:
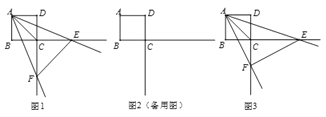
查看答案和解析>>【题目】已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别与边BC、DC的延长线交于点E、F,连接EF。设CE=a,CF=b。
(1)如图1,当∠EAF被对角线AC平分时,求a、b的值;
(2)当△AEF是直角三角形时,求a、b的值;
(3)如图3,探索∠EAF绕点A旋转的过程中a、b满足的关系式,并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】请阅读下列材料:问题:现有5个边长为1的正方形,排列形式如图甲,请把它们分割后拼接成一个新的正方形.要求:画出分割线并在正方形网格图(图中的每一个小正方形的边长均为1)中用实线画出拼接成的新正方形.
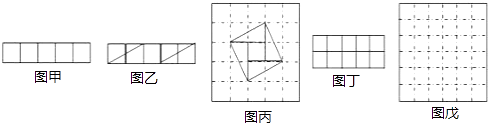
小东同学的做法是:设新正方形的边长为x(x>0),依题意,割补前后图形的面积相等,有x2=5,解得x=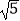 由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长.于是,画出如图乙所示的分割线,拼出如图丙所示的新的正方形.
由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长.于是,画出如图乙所示的分割线,拼出如图丙所示的新的正方形.
请你参考小东同学的做法,解决如下问题:
现有10个边长为1的小正方形,排列形式如图丁,请把它们分割后拼接成一个新的正方形.要求:在图丁中画出分割线,并在图戊的正方形网格图(图中的每一个小正方形的边长均为1)中用实线画出拼接成的新正方形.
说明:直接画出图形,不要求写分析过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠
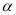 是锐角,∠
是锐角,∠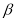 是钝角,且∠
是钝角,且∠ +∠
+∠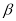 =180°,那么下列结论正确的是( )
=180°,那么下列结论正确的是( )A. ∠
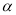 的补角和∠
的补角和∠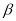 的补角相等 B. ∠
的补角相等 B. ∠ 的余角和∠
的余角和∠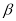 的补角相等
的补角相等C. ∠
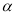 的余角和∠
的余角和∠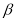 的补角互余 D. ∠
的补角互余 D. ∠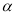 的余角和∠
的余角和∠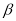 的补角互补
的补角互补 -
科目: 来源: 题型:
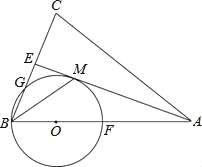
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
(1)求证:AE为⊙O的切线.
(2)当BC=8,AC=12时,求⊙O的半径.
(3)在(2)的条件下,求线段BG的长.
相关试题

