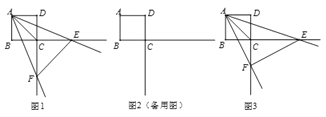
【题目】已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别与边BC、DC的延长线交于点E、F,连接EF。设CE=a,CF=b。
(1)如图1,当∠EAF被对角线AC平分时,求a、b的值;
(2)当△AEF是直角三角形时,求a、b的值;
(3)如图3,探索∠EAF绕点A旋转的过程中a、b满足的关系式,并说明理由。
参考答案:
【答案】(1)a=b=![]() ;(2)①当∠AEF=90°时,a=4,b=8,②当∠AFE=90°时,a=8,b=4;(3)ab=32,理由见解析.
;(2)①当∠AEF=90°时,a=4,b=8,②当∠AFE=90°时,a=8,b=4;(3)ab=32,理由见解析.
【解析】分析:(1)当∠EAF被对角线AC平分时,易证△ACF≌△ACE,因此CF=CE,即a=b.(2)分两种情况进行计算,①先用勾股定理得出CF2=8(CE+4)①,再用相似三角形得出4CF=CE(CE+4)②,两式联立解方程组即可;(3)先判断出∠AFD=∠CEF,再判断出AF=EF,从而得到△ADF≌△FCE即可.
本题解析:(1)∵四边形ABCD是正方形,∴∠ACF=∠DCD=90°,
∵AC是正方形ABCD的对角线,∴∠ACB=∠ACD=45°,∴∠ACF=∠ACE,
∵∠EAF被对角线AC平分,∴∠CAF=∠CAE,
在△ACF和△ACE中,
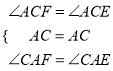 ,
,
∴△ACF≌△ACE,∴CE=CE,
∵CE=a,CF=b,∴a=b;
(2)当△AEF是直角三角形时,
①当∠AEF=90°时,△ABEF≌△ECF,∴a=4,b=8,
②当∠AFE=90°时,△ADF≌△FCE,∴a=8,b=4.
(3)ab=32,
理由:如图,
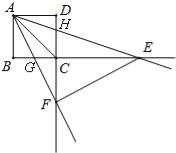
∵∠BAG+∠AGB=90°,∠AFC+∠CGF=90°,∠AGB=∠CGF,
∴∠BAG=∠AFC,
∵∠BAC=45°,
∴∠BAG+∠CAF=45°,
∴∠AFC+∠CAF=45°,
∵∠AFC+∠AEC=180°﹣(∠CFE+∠CEF)﹣∠EAF=180°﹣90°﹣45°=45°,
∴∠CAF=∠AEC,
∵∠ACF=∠ACE=135°,
∴△ACF∽△ECA,
∴![]() ,
,
∴EC×CF=AC2=2AB2=32
∴ab=32.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家推行“节能减排,低碳经济”政策后,某环保节能设备生产企业的产品供不应求.若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于90万元.已知这种设备的月产量x(套)与每套的售价
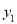 (万元)之间满足关系式
(万元)之间满足关系式 ,月产量x(套)与生产总成本
,月产量x(套)与生产总成本 (万元)存在如图所示的函数关系.
(万元)存在如图所示的函数关系.
(1)求月产量x的范围;
(2)如果想要每月利润为1750万元,那么当月产量应为多少套?
(3)如果每月获利润不低于1900万元,当月产量x(套)为多少时,生产总成本最低?并求出此时的最低成本.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正数m的两个不同平方根分别是2a-1与-a+2,则这个正数m=______
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为5,则正方形A,B,C,D的面积的和为
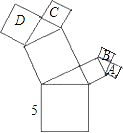
-
科目: 来源: 题型:
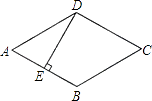
查看答案和解析>>【题目】如图,菱形ABCD的边长是4cm,E是AB的中点,且DE⊥AB,则菱形ABCD的面积为cm2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】请阅读下列材料:问题:现有5个边长为1的正方形,排列形式如图甲,请把它们分割后拼接成一个新的正方形.要求:画出分割线并在正方形网格图(图中的每一个小正方形的边长均为1)中用实线画出拼接成的新正方形.
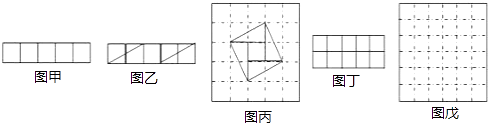
小东同学的做法是:设新正方形的边长为x(x>0),依题意,割补前后图形的面积相等,有x2=5,解得x=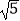 由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长.于是,画出如图乙所示的分割线,拼出如图丙所示的新的正方形.
由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长.于是,画出如图乙所示的分割线,拼出如图丙所示的新的正方形.
请你参考小东同学的做法,解决如下问题:
现有10个边长为1的小正方形,排列形式如图丁,请把它们分割后拼接成一个新的正方形.要求:在图丁中画出分割线,并在图戊的正方形网格图(图中的每一个小正方形的边长均为1)中用实线画出拼接成的新正方形.
说明:直接画出图形,不要求写分析过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠
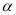 是锐角,∠
是锐角,∠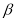 是钝角,且∠
是钝角,且∠ +∠
+∠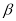 =180°,那么下列结论正确的是( )
=180°,那么下列结论正确的是( )A. ∠
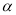 的补角和∠
的补角和∠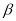 的补角相等 B. ∠
的补角相等 B. ∠ 的余角和∠
的余角和∠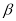 的补角相等
的补角相等C. ∠
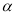 的余角和∠
的余角和∠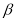 的补角互余 D. ∠
的补角互余 D. ∠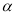 的余角和∠
的余角和∠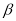 的补角互补
的补角互补
相关试题

