【题目】已知函数f(x)=xlnx﹣mx的图象与直线y=﹣1相切. (Ⅰ)求m的值,并求f(x)的单调区间;
(Ⅱ)若g(x)=ax3 , 设h(x)=f(x)﹣g(x),讨论函数h(x)的零点个数.
参考答案:
【答案】解:(I)设f(x)的图象与直线y=﹣1相切于点(x0 , ﹣1),(x0>0), f′(x)=lnx+1﹣m,(x>0)
则  即
即 
解得:x0=1,m=1,
由f′(x)=lnx>0得x>1;f′(x)=lnx<0得0<x<1;
所以函数f(x)的单调减区间为(0,1);增区间为(1,+∞),
(II)h(x)=f(x)﹣g(x)=xlnx﹣x﹣ax3=x(lnx﹣1﹣ax2)(x>0).
由h(x)=0得 ![]() ;
;
∴ ![]() .
.
记函数 ![]() ,
,
![]()
由r′(x)>0得 ![]() ;r′(x)<0得
;r′(x)<0得 ![]() ,
,
∴r(x)在  上单调递增;在
上单调递增;在  上单调递减,
上单调递减,
∴  ,
,
又  时,r(x)>0;x∈(0,e)时,r(x)<0;且x趋向于0时r(x)趋向于负无穷大.
时,r(x)>0;x∈(0,e)时,r(x)<0;且x趋向于0时r(x)趋向于负无穷大.
∴当a> ![]() 时,y=a与y=r(x)的图象无交点,函数h(x)无零点;
时,y=a与y=r(x)的图象无交点,函数h(x)无零点;
当a≤0或a= ![]() 时,y=a与y=r(x)的图象恰有一个交点,函数h(x)恰有一个零点;
时,y=a与y=r(x)的图象恰有一个交点,函数h(x)恰有一个零点;
当0<a< ![]() 时,y=a与y=r(x)的图象恰有两个交点,函数h(x)恰有两个个零点
时,y=a与y=r(x)的图象恰有两个交点,函数h(x)恰有两个个零点
【解析】(Ⅰ)确定函数的定义域,利用导数的几何意义,从而可求m的值和函数的单调区间;(Ⅱ)构造函数,利用导数,求出函数的最值,再分类讨论即可得到函数零点的个数
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性和函数的极值与导数的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,BD=2AD=8,AB=4
 .
. 
(Ⅰ)证明:平面PBD⊥平面PAD;
(Ⅱ)求二面角B﹣PA﹣D的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
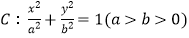 的离心率为
的离心率为 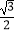 ,过左焦点F且垂直于x轴的直线与椭圆C相交,所得弦长为1,斜率为k(k≠0)的直线l过点(1,0),且与椭圆C相交于不同的两点A,B.
,过左焦点F且垂直于x轴的直线与椭圆C相交,所得弦长为1,斜率为k(k≠0)的直线l过点(1,0),且与椭圆C相交于不同的两点A,B.
(Ⅰ)求椭圆C的方程;
(Ⅱ)在x轴上是否存在点M,使得无论k取何值,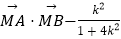 为定值?若存在,求出点M的坐标;若不存在,请说明理由.
为定值?若存在,求出点M的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,等边△ABC的边长为4cm,动点D从点B出发,沿射线BC方向移动,以AD为边作等边△ADE.
(1)在点D运动的过程中,点E能否移动至直线AB上?若能,求出此时BD的长;若不能,请说明理由;
(2)如图2,在点D从点B开始移动至点C的过程中,以等边△ADE的边AD、DE为边作ADEF.
①ADEF的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由;
②若点M、N、P分别为AE、AD、DE上动点,直接写出MN+MP的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为
 ,直线l的参数方程为
,直线l的参数方程为  (t为参数),直线l与曲线C1交于A,B两点. (Ⅰ)求|AB|的长度;
(t为参数),直线l与曲线C1交于A,B两点. (Ⅰ)求|AB|的长度;
(Ⅱ)若曲线C2的参数方程为 (α为参数),P为曲线C2上的任意一点,求△PAB的面积的最小值.
(α为参数),P为曲线C2上的任意一点,求△PAB的面积的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )

A.4.5
B.6
C.7.5
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f (x)=Asin(ωx+φ),(0<φ<π)的图象如图所示,若f(x0)=3,x0∈(
 ,
, 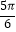 ),则sinx0的值为( )
),则sinx0的值为( ) 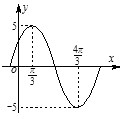
A.
B.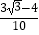
C.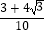
D.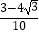
相关试题

