【题目】将两个大小不同的含30°角的三角板的直角顶点O重合在一起,保持△COD不动,将△AOB绕点O旋转,设射线AB与射线DC交于点F.
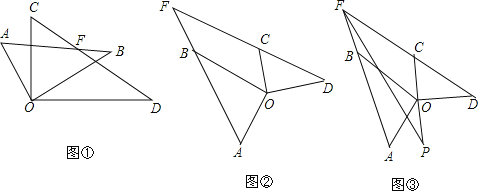
(1)如图①,若∠AOD=120°,
①AB与OD的位置关系 .
②∠AFC的度数= .
(2)如图②当∠AOD=130°,求∠AFC的度数.
(3)由上述结果,写出∠AOD和∠AFC的关系 .
(4)如图③,作∠AFC、∠AOD的角平分线交于点P,求∠P的度数.
参考答案:
【答案】(1)①AB∥OD;②30°;(2)40°;(3)∠AOD=∠AFC+90°;(4)15°.
【解析】
(1)①先求出∠BOD=30°,从而得到∠B=∠BOD,再根据内错角相等,两直线平行解答;
②根据两直线平行,同位角相等解答即可;
(2)根据周角求出∠BOC,根据邻补角求出∠OBF和∠OCF,然后根据四边形的内角和定理列式计算即可得解;
(3)根据计算的度数写出关系式即可;
(4)设OB、PF相交于G,然后根据三角形的内角和定理列式整理即可得解.
(1)①∵∠AOD=120°,
∴∠BOD=∠AOD-∠AOB=120°-90°=30°;
∴∠B=∠BOD,
∴AB∥OD;
②∵AB∥OD,
∴∠AFC=∠D=30°;
(2)∵∠AOD=130°,
∴∠BOC=360°-130°-90°×2=50°,
又∵∠OBF=180°-30°=150°,∠OCF=180°-60°=120°,
∴∠AFC=360°-150°-120°-50°=40°;
(3)∠AOD=∠AFC+90°;
(4)设OB、PF相交于G,
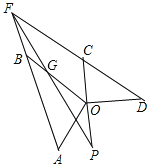
∵∠AFC、∠AOD的角平分线交于点P,
∴∠BFG=![]() ∠AFC,∠AOP=
∠AFC,∠AOP=![]() ∠AOD,
∠AOD,
在△BFG和△OGP中,∠BFG+∠OBF=∠POG+∠P,
∴![]() ∠AFC+150°=
∠AFC+150°=![]() ∠AOD+90°+∠P,
∠AOD+90°+∠P,
∴![]() ∠AFC+150°=
∠AFC+150°=![]() (∠AFC+90°)+90°+∠P,
(∠AFC+90°)+90°+∠P,
整理得,∠P=15°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在□ABCD中,点E,F分别在边BC和AD上,且CE=AF,
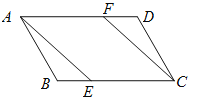
(1)求证:△ABE ≌ △CDF;
(2)求证:四边形AECF是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系xOy中,正比例函数y=
 x的图象经过点A,点A的纵坐标为4,反比例函数y=
x的图象经过点A,点A的纵坐标为4,反比例函数y=  的图象也经过点A,第一象限内的点B在这个反比例函数的图象上,过点B作BC∥x轴,交y轴于点C,且AC=AB.求:
的图象也经过点A,第一象限内的点B在这个反比例函数的图象上,过点B作BC∥x轴,交y轴于点C,且AC=AB.求:
(1)这个反比例函数的解析式;
(2)直线AB的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需要的时间与原计划生产450台机器所需要的时间相同.
(1)原计划平均每天生产多少台机器?
(2)若该工厂要在不超过5天的时间,生产1100台机器,则平均每天至少还要再多生产多少台机器?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E是BC上一点,直线AE交BD于点M,交DC的延长线于点F,G是EF的中点,连接CG.求证:
(1)△ABM≌△CBM;
(2)CG⊥CM.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市用3000元购进某种干果销售,由于销售状况良好,超市又调拨9000元资金购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量是第一次的2倍还多300千克,如果超市按每千克9元的价格出售,当大部分干果售出后,余下的600千克按售价的8折售完.
(1)该种干果的第一次进价是每千克多少元?
(2)超市销售这种干果共盈利多少元?
相关试题

