搜索
【题目】在同样条件下对某种小麦种子进行发芽试验，统计发芽种子数，获得如下频数表．
试验种子n（粒） | 1 | 5 | 50 | 100 | 200 | 500 | 1000 | 2000 | 3000 |
发芽频数m | 1 | 4 | 45 | 92 | 188 | 476 | 951 | 1900 | 2850 |
发芽频率 | 0 | 0.80 | 0.90 | 0.92 | 0.94 | 0.952 | 0.951 | a | b |
（1）计算表中a，b的值；
（2）估计该麦种的发芽概率；
（3）如果该麦种发芽后，只有87%的麦芽可以成活，现有100kg麦种，则有多少千克的麦种可以成活为秧苗？
参考答案：
【答案】（1）0.95，0.95（2）0.95（3）82.65kg
【解析】因为发芽频率=
,所以
；
根据图表可知发芽频率趋于0.95平稳，故估计麦种发芽的概率为0.95；
因为该麦种发芽后，只有87%的麦芽可以成活，所以可成活麦种质量为：
-
科目： 来源： 题型：
查看答案和解析>>【题目】某学习小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，绘制了如下的表格，则符合这一结果的实验最有可能的是（ ）
实验次数
100
200
300
500
800
1000
2000
频率
0．365
0．328
0．330
0．334
0．336
0．332
0．333
A．一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃
B．在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀”
C．抛一个质地均匀的正六面体骰子，向上的面点数是5
D．抛一枚硬币，出现反面的概率
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义新运算：对于任意实数a，b，都有a
b＝a(a－b)＋1，等式右边是通常的加法、减法及乘法运算，比如：2
5＝2×(2－5)＋1＝2×(－3)＋1＝－6＋1＝－5.(1)求(－2)
3的值；(2)若3
x的值小于13，求x的取值范围，并在如图所示的数轴上表示出来．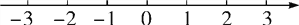
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，D在AB上，E在AC上，下列条件中，能判定DE//BC的是（ ）
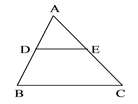
A.
B. 
C.
D.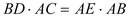 
-
科目： 来源： 题型：
查看答案和解析>>【题目】为加强中小学生安全和禁毒教育，某校组织了“防溺水、交通安全、禁毒”知识竞赛，为奖励在竞赛中表现优异的班级，学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同，每个篮球的价格相同)，购买1个足球和1个篮球共需159元；足球单价是篮球单价的2倍少9元．
(1)求足球和篮球的单价各是多少元；
(2)根据学校实际情况，需一次性购买足球和篮球共20个，但要求购买足球和篮球的总费用不超过1550元，学校最多可以购买多少个足球？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某公交公司有A，B型两种客车，它们的载客量和租金如下表：
A
B
载客量(人/辆)
45
30
租金(元/辆)
400
280
红星中学根据实际情况，计划租用A，B型客车共5辆，同时送七年级师生到基地参加社会实践活动，设租用A型客车x辆，根据要求回答下列问题：
(1)用含x的式子填写下表：
车辆数(辆)
载客量(人)
租金(元)
A
x
45x
400x
B
5－x
(2)若要保证租车费用不超过1900元，求x的最大值；
(3)在(2)的条件下，若七年级师生共有195人，写出所有可能的租车方案，并确定最省钱的租车方案．
-
科目： 来源： 题型：
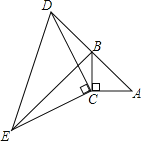
查看答案和解析>>【题目】如图，在△ABC中，∠ACB=90°，AC=BC，延长AB至点D，使DB=AB，连接CD，以CD为直角边作等腰直角三角形CDE，其中∠DCE=90°，连接BE.
（1）求证：△ACD≌△BCE；
（2)若AC=3，求BE的长度.
相关试题
