【题目】定义新运算:对于任意实数a,b,都有a![]() b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如:2
b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如:2![]() 5=2×(2-5)+1=2×(-3)+1=-6+1=-5.
5=2×(2-5)+1=2×(-3)+1=-6+1=-5.
(1)求(-2) ![]() 3的值;
3的值;
(2)若3![]() x的值小于13,求x的取值范围,并在如图所示的数轴上表示出来.
x的值小于13,求x的取值范围,并在如图所示的数轴上表示出来.
![]()
参考答案:
【答案】(1)11;(2)x>-1.
【解析】试题分析:(1)按照定义新运算a⊕b=a(a-b)+1,求解即可;
(2)先按照定义新运算a⊕b=a(a-b)+1,得出3⊕x,再令其小于13,得到一元一次不等式,解不等式求出x的取值范围,即可在数轴上表示.
试题解析:(1)∵a⊕b=a(a-b)+1,
∴(-2)⊕3=-2×(-2-3)+1=10+1=11; (2)∵3⊕x<13,
∴3(3-x)+1<13,
∴9-3x+1<13,
∴-3x<3,
∴x>-1.
在数轴上表示如下.
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①、②、③、○n、…、M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连接OM、ON.

(1)求图①中∠MON的度数;
(2)图②中∠MON的度数是_________,图③中∠MON的度数是___________;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小李以0.8元/kg的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完,销售金额与销售量之间的关系如图所示,那么小李赚了__________元
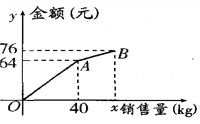
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.抛一个质地均匀的正六面体骰子,向上的面点数是5
D.抛一枚硬币,出现反面的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D在AB上,E在AC上,下列条件中,能判定DE//BC的是( )
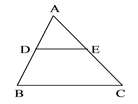
A.
 B.
B. 
C.
 D.
D. 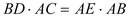
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同样条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表.
试验种子n(粒)
1
5
50
100
200
500
1000
2000
3000
发芽频数m
1
4
45
92
188
476
951
1900
2850
发芽频率
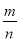
0
0.80
0.90
0.92
0.94
0.952
0.951
a
b
(1)计算表中a,b的值;
(2)估计该麦种的发芽概率;
(3)如果该麦种发芽后,只有87%的麦芽可以成活,现有100kg麦种,则有多少千克的麦种可以成活为秧苗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元;
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
相关试题

