【题目】如图所示,在直角梯形ABCD中,AD∥BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒). 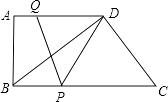
(1)设△DPQ的面积为S,求S与t之间的函数关系式;
(2)当t为何值时,四边形PCDQ是平行四边形?
(3)分别求出当t为何值时,①PD=PQ,②DQ=PQ.
参考答案:
【答案】
(1)解:直角梯形ABCD中,AD∥BC,∠A=90°,BC=21,AB=12,AD=16,
依题意AQ=t,BP=2t,则DQ=16﹣t,PC=21﹣2t,
过点P作PE⊥AD于E,

则四边形ABPE是矩形,PE=AB=12,
∴S△DPQ= ![]() DQAB=
DQAB= ![]() (16﹣t)×12=﹣6t+96
(16﹣t)×12=﹣6t+96
(2)解:当四边形PCDQ是平行四边形时,PC=DQ,
∴21﹣2t=16﹣t解得:t=5,
∴当t=5时,四边形PCDQ是平行四边形
(3)解:∵AE=BP=2t,PE=AB=12,
①当PD=PQ时,QE=ED= ![]() QD,
QD,
∵DE=16﹣2t,
∴AE=BP=AQ+QE,即2t=t+16﹣2t,
解得:t= ![]() ,
,
∴当t= ![]() 时,PD=PQ
时,PD=PQ
②当DQ=PQ时,DQ2=PQ2
∴t2+122=(16﹣t)2解得:t= ![]()
∴当t= ![]() 时,DQ=PQ
时,DQ=PQ
【解析】(1)S△QDP= ![]() DQAB,由题意知:AQ=t,DQ=AD﹣AQ=16﹣t,将DQ和AB的长代入,可求出S与t之间的函数关系式;(2)当四边形PCDQ为平行四边形时,PC=DQ,即16﹣t=21﹣2t,可将t求出;(3)当PD=PQ时,可得:AD=3t,从而可将t求出;当DQ=PQ时,根据DQ2=PQ2即:t2+122=(16﹣t)2可将t求出.
DQAB,由题意知:AQ=t,DQ=AD﹣AQ=16﹣t,将DQ和AB的长代入,可求出S与t之间的函数关系式;(2)当四边形PCDQ为平行四边形时,PC=DQ,即16﹣t=21﹣2t,可将t求出;(3)当PD=PQ时,可得:AD=3t,从而可将t求出;当DQ=PQ时,根据DQ2=PQ2即:t2+122=(16﹣t)2可将t求出.
【考点精析】通过灵活运用勾股定理的概念和平行四边形的判定与性质,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知∠AOB=120°,∠COD=60°,OM在∠AOC内,ON在∠BOD内,∠AOM=
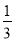 ∠AOC,∠BON=
∠AOC,∠BON=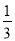 ∠BOD.
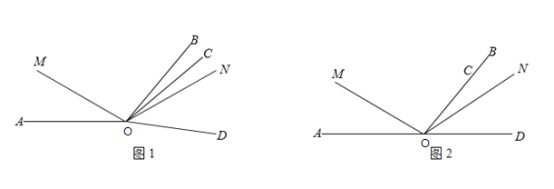
∠BOD.(1)∠COD从图1中的位置绕点O逆时针旋转到OC与OB重合时,如图2,∠MON= °;
(2)∠COD从图2中的位置绕点O逆时针旋转n°(0<n<120且n≠60),求∠MON的度数;
(3)∠COD从图2中的位置绕点O逆时针旋转n°(0<n<120),则n= 时,∠MON=2∠BOC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆形靠在墙角的截面图,A、B分别为⊙O的切点,BC⊥AC,点P在
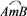 上以2°/s的速度由A点向点B运动(A、B点除外),连接AP、BP、BA。
上以2°/s的速度由A点向点B运动(A、B点除外),连接AP、BP、BA。(1)当∠PBA=28°,求∠OAP的度数;
(2)若点P不在AO的延长线上,请写出∠OAP与∠PBA之间的关系;
(3)当点P运动几秒时,△APB为等腰三角形.
-
科目: 来源: 题型:
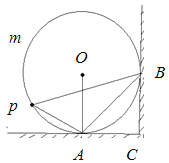
查看答案和解析>>【题目】我市某校在八,九年级开展征文活动,校学生会对这两个年级各班内的投稿情况进行统计,并制成了如图所示的两幅不完整的统计图.
(1)求扇形统计图中投稿篇数为2所对应的扇形的圆心角的度数:
(2)求该校八,九年级各班在这一周内投稿的平均篇数,并将该条形统计图补充完整.
(3)在投稿篇数为9篇的4个班级中,八,九年级各有两个班,校学生会准备从这四个中选出两个班参加全市的表彰会,求出所选两个班正好不在同一年级的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(-c)3·(-c)2m+1=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )
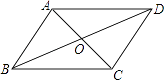
A.AB∥DC,AD=BC
B.AB∥DC,AD∥BC
C.AB=DC,AD=BC
D.OA=OC,OB=OD -
科目: 来源: 题型:
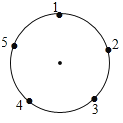
查看答案和解析>>【题目】如图是一个圆,一只电子跳蚤在标有五个数字的点上跳跃,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若跳蚤从2这点开始跳,则经2017次跳后它停在数____对应的点上.
相关试题

