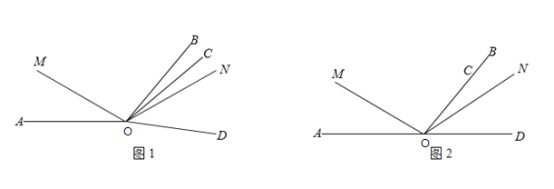
【题目】如图1,已知∠AOB=120°,∠COD=60°,OM在∠AOC内,ON在∠BOD内,∠AOM=![]() ∠AOC,∠BON=
∠AOC,∠BON=![]() ∠BOD.
∠BOD.
(1)∠COD从图1中的位置绕点O逆时针旋转到OC与OB重合时,如图2,∠MON= °;
(2)∠COD从图2中的位置绕点O逆时针旋转n°(0<n<120且n≠60),求∠MON的度数;
(3)∠COD从图2中的位置绕点O逆时针旋转n°(0<n<120),则n= 时,∠MON=2∠BOC.
参考答案:
【答案】(1)100°;(2)100°;(3)50或70.
【解析】试题分析:(1)由∠MON=![]() ∠AOB+
∠AOB+![]() ∠COD代入即可得到结论;
∠COD代入即可得到结论;
(2)分两种情况讨论:①当0<n<60°时,∠AOC=∠AOB-∠BOC=120°-n,∠BOD=60°-n,由∠MON=∠MOC+∠COB+∠BON,代入即可得到结论;
②当60°<n<120°时,∠AOC=120°-n,∠COD=60°,∠BOD=n-60°,∠MOC=![]() ∠AOC,∠DON=
∠AOC,∠DON=![]() ∠BOD,由∠MON=∠MOC+∠COD+∠DON,代入即可得到结论.
∠BOD,由∠MON=∠MOC+∠COD+∠DON,代入即可得到结论.
(3)分两种情况讨论:①当0<n<60°时,∠BOC=n,∠MON=2n,由∠MON=![]() (120°+n)+60°-
(120°+n)+60°-![]() (60°+n)=100°,解方程即可得到结论;
(60°+n)=100°,解方程即可得到结论;
②当60°<n<120°时,∠AOC=360°-(120°+n)=240°-n,∠BOD=60°+n,由∠MON=360°-∠AOM-∠AOB-∠BON=360°-![]() (240°-n)-120°-
(240°-n)-120°-![]() (60°+n)=140°,解方程即可得到结论.
(60°+n)=140°,解方程即可得到结论.
试题解析:解:(1)∠MON=![]() ∠AOB+
∠AOB+![]() ∠COD=100°;
∠COD=100°;
(2)①当0<n<60°时,∠AOC=∠AOB-∠BOC=120°-n,∠BOD=60°-n,∴∠MON=∠MOC+∠COB+∠BON=![]() ∠AOC+n+
∠AOC+n+![]() ∠BOD=
∠BOD=![]() (120°-n)+n+
(120°-n)+n+![]() (60°-n)=100°;
(60°-n)=100°;

②当60°<n<120°时,∠AOC=120°-n,∠COD=60°,∠BOD=n-60°,∠MOC=![]() ∠AOC,∠DON=
∠AOC,∠DON=![]() ∠BOD,∴∠MON=∠MOC+∠COD+∠DON=
∠BOD,∴∠MON=∠MOC+∠COD+∠DON=![]() (120°-n)+60°+
(120°-n)+60°+![]() (n-60°)=100°.
(n-60°)=100°.

综上所述:∠MON的度数恒为100°.
(3)①当0<n<60°时,∠BOC=n,∠MON=2n,∴∠MON=![]() (120°+n)+60°-
(120°+n)+60°-![]() (60°+n)=100°;解得:n=50°;
(60°+n)=100°;解得:n=50°;

②当60°<n<120°时,∠AOC=360°-(120°+n)=240°-n,∠BOD=60°+n,∴∠MON=360°-∠AOM-∠AOB-∠BON=360°-![]() (240°-n)-120°-
(240°-n)-120°-![]() (60°+n)=140°,解得:n=70°.
(60°+n)=140°,解得:n=70°.

综上所述:n=50°或70°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若m为大于0的整数,则(m+4)2-(m-4)2一定是()
A. 2的倍数,B. 4的倍数,C. 8的倍数,D. 16的倍数
-
科目: 来源: 题型:
查看答案和解析>>【题目】若4x2+(a-1)xy+9y2是完全平方式,则a的值是 ( )
A. 7或-5B. 13或-11C. -13或14D. -7或-5
-
科目: 来源: 题型:
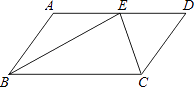
查看答案和解析>>【题目】如图,在平行四边形ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=12cm,CE=5cm,求平行四边形ABCD的周长.
-
科目: 来源: 题型:
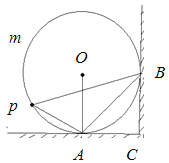
查看答案和解析>>【题目】如图,圆形靠在墙角的截面图,A、B分别为⊙O的切点,BC⊥AC,点P在
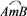 上以2°/s的速度由A点向点B运动(A、B点除外),连接AP、BP、BA。
上以2°/s的速度由A点向点B运动(A、B点除外),连接AP、BP、BA。(1)当∠PBA=28°,求∠OAP的度数;
(2)若点P不在AO的延长线上,请写出∠OAP与∠PBA之间的关系;
(3)当点P运动几秒时,△APB为等腰三角形.
-
科目: 来源: 题型:
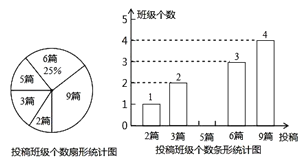
查看答案和解析>>【题目】我市某校在八,九年级开展征文活动,校学生会对这两个年级各班内的投稿情况进行统计,并制成了如图所示的两幅不完整的统计图.
(1)求扇形统计图中投稿篇数为2所对应的扇形的圆心角的度数:
(2)求该校八,九年级各班在这一周内投稿的平均篇数,并将该条形统计图补充完整.
(3)在投稿篇数为9篇的4个班级中,八,九年级各有两个班,校学生会准备从这四个中选出两个班参加全市的表彰会,求出所选两个班正好不在同一年级的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在直角梯形ABCD中,AD∥BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).
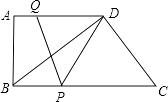
(1)设△DPQ的面积为S,求S与t之间的函数关系式;
(2)当t为何值时,四边形PCDQ是平行四边形?
(3)分别求出当t为何值时,①PD=PQ,②DQ=PQ.
相关试题

