【题目】如图在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A、D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
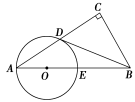
(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
参考答案:
【答案】(1)、证明过程见解析;(2)、5.
【解析】
试题分析:(1)、连接OD,根据△AOD为等腰三角形可得∠A=∠ODA,根据∠A+∠CDB=90°可得∠ODA+∠CDB=90°,从而得出∠BDO=90°;(2)、连接OE,根据直径所对的圆周角为直角得出∠ADE=90°,根据D为中点可得E为AB的中点,根据△ADE和△ACB相似可得AC:AB=4:5,然后求出BC的长度,从而得出直径的长度.
试题解析:(1)、连接OD,在△AOD中,OA=OD, ∴∠A=∠ODA,
又∵∠A+∠CDB=90° ∴∠ODA+∠CDB=90°, ∴∠BDO=180°-90°=90°,即OD⊥BD,
∴BD与⊙O相切.
(2)、连接DE,∵AE是⊙O的直径, ∴∠ADE=90°, ∴DE∥BC.
又∵D是AC的中点,∴AE=BE. ∴△AED∽△ABC.
∴AC∶AB=AD∶AE. ∵AD:AE=4:5 ∴AC∶AB=4∶5,
令AC=4x,AB=5x,则BC=3x. ∵BC=6,∴AB=10,
∴AE=5,∴⊙O的直径为5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③2a﹣b=0;④8a+c<0;⑤9a+3b+c<0,其中结论正确有( )个。

A.2个 B.3个 C.4个 D.5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标平面内,直线y=-x+5与
 轴和
轴和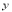 轴分别交于A、B两点,二次函数y=
轴分别交于A、B两点,二次函数y=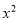 +bx+c的图象经过点A、B,且顶点为C.
+bx+c的图象经过点A、B,且顶点为C.
(1)求这个二次函数的解析式;
(2)求sin∠OCA的值;
(3)若P是这个二次函数图象上位于x轴下方的一点,且
 ABP的面积为10,求点P的坐标.
ABP的面积为10,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】“平行四边形的对角线互相垂直”是事件.(填“必然”、“随机”、“不可能”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB与A′B′分别是☉O与☉O′的两条弦,AB=A′B′,那么∠AOB与∠A′O′B′的大小关系是( )
A. ∠AOB=∠A′O′B′ B. ∠AOB>∠A′O′B′ C. ∠AOB<∠A′O′B′ D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】一条弦把圆分成1:3两部分,则弦所对的圆心角为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】要想了解10万名考生的数学成绩,从中抽取了2000名考生的数学成绩进行统计分析,以下说法正确的是( )
A.这2000名考生是总体的一个样本
B.每位考生的数学成绩是个体
C.10万名考生是总体
D.2000名考生是样本的容量
相关试题

